信息论基础
离散随机变量的信息度量
$$ H(X) = \mathbf E\{H(X=x_i)\} = -\sum_i p_i \log p_i $$称为熵
单位:
- 2 (Bit)
- e (Nat)
- 10 (Hartely)
表示了信息描述的有效性极限
信源编码(Source Coding),通过信息的有效表示,提高通信的有效性。例如: Huffman 编码
离散随机变量的最大熵: $\max_{p_i} H(X) = \log|S|$
前缀码:任何码字都不是其他码字的前缀。前缀码保证了唯一可译码。是二叉树叶子节点。
Kraft不等式
对于信源字符集 $\lbrace a_1, \dots, a_m\rbrace$ ,必满足:
$$ \sum\limits_{k=1}^{M}2^{-l(a_k)} \le 1 $$同时,若上式成立,必存在码长分别为 $𝑙(𝑎_𝑘)$ 的前缀码。
最小前缀码的平均码长:
$$ \min \bar L =\sum\limits_{i=1}^{M}p_il_i\\ s.t.\sum\limits_{i=1}^{M} 2^{-l_i} = 1 $$由拉格朗日乘子法
$$ p_i = 2^{-l_i}, \bar L_{min} = -\sum\limits_{i=1}^{M}p_i \log p_i $$记 $H(X) = -\sum p_i\log p_i$ .一般的,上下界为 $H(X) \le \bar L \lt H(X) + 1$ .
如果我们将 $k$ 个独立同分布的信源符号 $x_1, \dots, x_k$ 堪称一个,对整体应用前缀码编码:
$$ \begin{align*} H(X_1, \dots, X_k) &= -\sum P(x_1, \dots, x_k) \log P(x_1, \dots, x_k)\\ &= -\sum P(x_1, \dots, x_k) [\log P(x_1) + \dots + \log(x_k)]\\ &= -\sum P(x_1)\log (x_1) - \dots - \sum P(x_k)\log (x_k)\\ &= -kH(X) \end{align*} $$直观:对长度为 $𝑛$ 的 $M$ 种信源符号序列, $𝑥_𝑖$ 出现的次数 $≈𝑛𝑝_𝑖$
典型序列应满足上述分布,否则就“小众”“非典型”
典型的个数 # $≈ \frac{𝒏!}{(𝑛𝑝_1) !… (𝑛𝑝_M) !}$
平均每个信源符号可以用 $L = \frac{1}{n}\log\left(\frac{𝒏!}{(𝑛𝑝_1) !… (𝑛𝑝_M) !}\right)$ 个 bit 来表达。
通过 Stirling 公式可以得出 L的上下界。
故
$$ \lim\limits_{n\rightarrow \infty}^{} L = H(X) $$最大熵
离散型随机变量的最大熵为
$$ \max_{p_i} H(X) = \log |S| $$可以用梯度法直观感受,当所有分量的概率相等时,熵最大。
联合熵
联合概率
$$ p_{i, j} = \text{Pr}\lbrace X = x_i, Y = y_j\rbrace $$联合熵的定义:
$$ H(XY) = -\sum\limits_{i}^{}\sum\limits_{j}^{} p_{i, j} \log p_{i, j} $$条件熵
条件概率
$$ p_{i\mid j} = \text{Pr}\lbrace X = x_i \mid Y = y_j\rbrace $$条件熵的定义:
$$ H(X|Y) = -\sum\limits_{i}^{}\sum\limits_{j}^{} p_{i, j} \log p_{i\mid j} $$通过相关观测进行无损压缩,若观测到 $Y = \alpha_j$ :
$$ \bar L(\alpha_j) = -\sum\limits_{i}^{}\sum\limits_{j}^{} p_{i\mid j} \log p_{i\mid j} $$于是
$$ \bar L =-\sum\limits_{j=1}^{N} \bar L(\alpha_j)p_j = -\sum\limits_{j=1}^{N}p_j\sum\limits_{i=1}^{M}p_{i|j} \log(p_{i|j}) = -\sum\limits_{i=1}^{M}\sum\limits_{j=1}^{N}p_{ij}\log(p_{i|j}) = H(X|Y) $$链式法则
$$ H(XY) = H(Y) + H(X|Y) $$两个随机变量的联合不确定性=一个随机变量的不确定性+知道这个随机变量后另一个随机变量残余的不确定性
互信息(Mutual Infomation)
$$ \begin{align*} I(X;Y) &= H(X) + H(Y) - H(XY)\\ &= H(X) - H(X|Y) \\ &= H(Y) - H(Y|X) \end{align*} $$互信息的物理意义
第一种理解:
- X的不确定度减去观测Y后X残存的不确定度
- 即:通过观测Y带来的帮助了解X的信息
第二种理解:
- Y的不确定度减去观测X后Y残存的不确定度
- 即:通过观测X带来的帮助了解Y的信息
若 $X, Y$ 相互独立,记为 $X\perp Y$ ,则 $I(X;Y) = 0$ , $H(X) = H(X|Y)$ , $H(Y) = H(Y|X)$ 。观测一个随机变量完全无助于了解另一个随机变量。
- $H(XY) = H(X) + H(Y)$ ,总平均码长等于各自平均码长之和。
若 $X = Y$ ,则 $I(X;Y) = H(X) = H(Y)$ , $H(X|Y) = H(Y|X) = 0$ 。观测一个随机变量完全了解另一个随机变量。
$H(XY) = H(Y) + H(X|Y) = H(Y)$ ,只需要编码其中一个即可。 $$ X \perp Y \leftrightarrow H(X + Y | X) = H(Y | X) = H(Y), H(X + Y, X) = H(Y , X) $$ $$ H(X + X | X) = H(X | X) = 0, H(X + X, X) = H(X , X) = H(X) $$信息传输的基本模型
- 信息通道,简称信道(Channel)对于输入符号有随机扰动,本质上可用一组条件概率表示
- 限于物理条件,信宿只能观测信道输出 $Y$ ,由此了解其输入 $X$
- 通过观测Y可以获得的关于X的信息量是 $I(X;Y)$
信息传输的优化
目标:最大化发送端 $X$ 和接收方 $Y$ 的互信息
方法:
- 信道是由物理实现所决定的,无法控制
- 但是可以选择X的概率分布
因此有如下优化问题:
$$ p*_i = \argmax_{\sum_i p_i = 1, p_i \ge 0} I(X;Y) $$定义信道容量 $C = \max_{\sum_i p_i = 1, p_i \ge 0} I(X;Y)$
信道容量的物理意义
- 平均每个信道符号所能传的最大的信息量
- 或:单位时间内信道所传最大的信息量
优化问题的表达式
$$ p_i^* = \argmax_{\sum_i p_i = 1, p_i \ge 0} - \sum_i\sum_j p_i p_{j|i} \log \frac{\sum\limits_i p_i p_{j|i}}{p_{j|i}} $$信道容量不易计算
对称二进制信道(BSC)
- 一种典型信道模型
- 分析信道编码时有很多应用
利用互信息表达式
$$ \begin{align*} I(X;Y) &= H(Y) - H(Y | X)\\ &= H(Y) - \sum_i p_i \left[-\sum_j p_{j|i} \log p_{j|i}\right]\\ &= H(Y) - [-\varepsilon\log \varepsilon - (1 - \varepsilon)\log(1 - \varepsilon)]\\ &\le 1 - [-\varepsilon\log \varepsilon - (1 - \varepsilon)\log(1 - \varepsilon)] = C\\ \end{align*}\\ Y \sim \begin{bmatrix} 0 & 1\\ 1/2 & 1/2 \end{bmatrix} $$如果误码率 $\varepsilon = 0.5$ ,则信道容量为0, 传递不了信息。
如果误码率 $\varepsilon > 0.5$ ,继续增大差错率,反而可以提高信道容量。
高斯信道
$$ Y = X + N\\ f_N(n) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp\left(-\frac{(y - x)^2}{2\sigma^2}\right) $$

Shannon 公式
$$ C = W\log(1 + \frac{P}{Wn_0}) $$连续性随机变量的熵
$$ H(X) = - \int\limits_{-\infty}^{\infty}p(x)\log p(x) \mathrm dx + \lim_{\Delta \rightarrow 0} \log \frac{1}{\Delta} $$我们只关心相对不确定性,定义微分熵
$$ h(X) = -\int\limits_{-\infty}^{\infty}p(x) \log p(x)\mathrm dx $$微分熵是对连续型变量相对不确定性的一种描述
- 其定义剔除了连续性或“精准要求”带来的困难,保
留了分布函数形状自身的特征 - 它说明用有限字符集合的字符串描述连续分布的随机
变量,则平均字符长度为无穷大 - 为了用有限长字符串描述信源,需要进行有损压缩,
从而带来失真,即原始信源和压缩结果之间的差异 - 失真测度包括:均方误差,绝对值误差,主观误差等
- 对于图像,视频和语音等连续信源的编码等均属于有
损压缩
多元随机变量的熵
联合熵:
$$ h(XY) = -\int\limits_{-\infty}^{\infty}p(x, y) \log p(x, y)\mathrm dx \mathrm{d}y $$条件熵:
$$ h(Y|X) = -\int\limits_{-\infty}^{\infty}p(x, y) \log p(y|x)\mathrm dx \mathrm{d}y $$互信息:
$$ \begin{align*} I(X;Y) &= h(X) + h(Y) - h(XY)\\ &= h(X) - h(X|Y) \\ &= h(Y) - h(Y|X) \end{align*} $$压缩编码
压缩编码的分类
- 无损压缩
- 输入:数字序列
- 输出:数字序列
- 目的:使得平均长度更小
- 有损压缩
- 输入:模拟信号
- 输出:数字序列
- 目的:实现数字传输
信号压缩编码的步骤:
- 抽样
- 量化
- 压缩编码
抽样
连续时间信源的离散化

离散化的方式:在标准正交基上投影展开
$$ s(t) = \sum_k a_k\phi_k(t)\\ a_k = <s(t), \phi_k(t)> $$若 $s(t)$ 是时限信号(宽度 $T$ ),可以用傅里叶展开的系数作为离散化结果: $s(t) = \sum\limits_k a_k e^{2\pi jkt/T}$
若 $s(t)$ 是带限信号(带宽 $W$ ),可以在频域对 $\hat S(f)$ 做傅里叶展开:
$$ \hat S(f) = \sum\limits_k \alpha_k e^{2\pi jkf/(2W)} $$变换回时域时,得到 Nyquist 抽样定理:
$$ s(t) =\sum\limits_{k}^{}s(kT) \text{sinc}\left(\left(\frac{t}{T} - k\right)\right), T = \frac{1}{2W} $$频域无混叠等价于时域无畸变
对于带通采样,有无混叠条件:
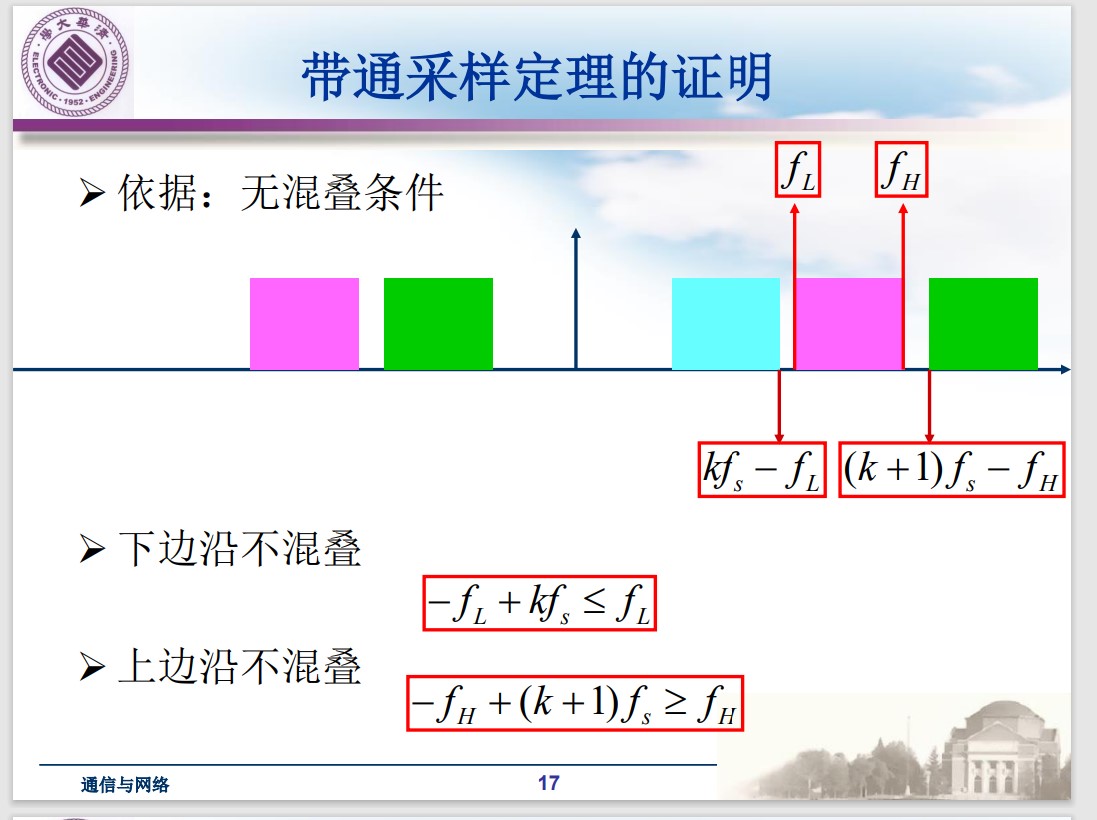
可以推导得出:
$$ f_s = 2B\left(1 + \frac{M}{N}\right)\\ N = \left\lfloor\frac{f_H}{B}\right\rfloor\\ M = \left\lbrace\frac{f_H}{B}\right\rbrace\\ B = f_H - f_L $$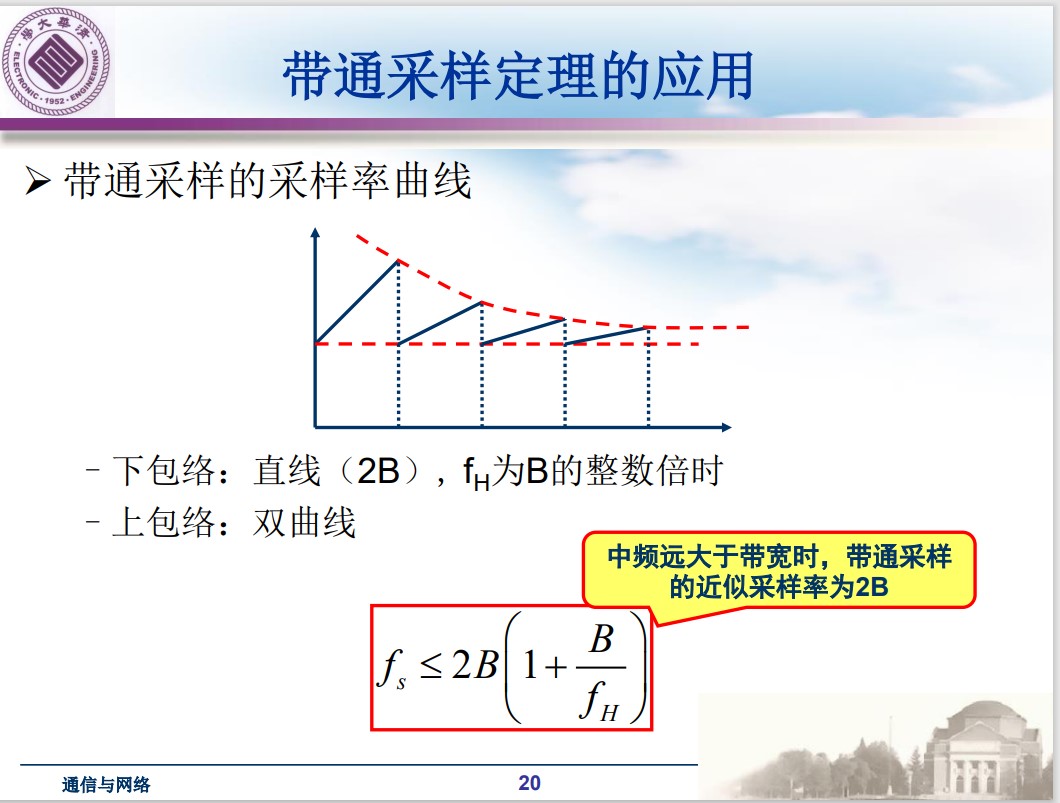
横轴为 $f_H/B$ ,纵轴为 $f_s$
量化
分层电平: $\lbrace x_k \lt x \le x_{k + 1} \rbrace$
重建/输出电平: $y_k$ 代表一个量化区间,用以重构信号时使用的电平值
量化函数: $y = Q(x)$ , $y_k = Q\lbrace x_k \lt x \le x_{k + 1} \rbrace$
量化间隔: $\Delta_k = x_{k + 1} - x_{k}$
均匀量化 & 非均匀量化
均匀量化只对有界随机变量存在
量化
- 在此只讨论标量的量化
- 量化噪声: $q = x - y = x - Q(x)$
- 量化噪声是一个随机变量
- 方差 $\sigma_q^2 = \int_{-\infty}^{\infty}[x - Q(x)]^2p_x(x)\mathrm dx$
- 方差与输入信号分布有关,不存在普适的最佳量化方案
量化噪声的计算
$$ \sigma_q^2 =\sum\limits_{k=1}^{L}\int_{x_k}^{x_{k + 1}}(x - y_k)^2p_x(x)\mathrm dx $$从较容易的情况着手
- 只考虑电平区间 $[-V,V]$ 之间的信号,并假设量化间隔很小,亦即分层电平很密
- 在实际情况中,信号的分布函数处处可导,此时每个量化区间内信号的条件分布为均匀分布
量化区间内,近似概率密度 $p_x(x) = \frac{P_k}{\Delta_k}$
密集分层的量化噪声近似
$$ \sigma_{qn}^2 = \sum\limits_{k=1}^{L}\int_{x_k}^{x_{k + 1}}(x - y_k)^2p_x(x)\mathrm dx = \sum\limits_{k=1}^{L}\frac{P_k}{\Delta_k}\int_{x_k}^{x_{k + 1}}(x - y_k)^2\mathrm dx = \frac{1}{12}\sum_{k = 1}^L P_k\Delta_k^2 = \frac{1}{12} \int_{-V}^{V}(\Delta_k)^2p_x(x)\mathrm dx $$若 $\Delta_k = \Delta$ ,
$$ \sigma_{qn}^2 = \frac{1}{12}\sum_k P_k\Delta_k^2 = \frac{\Delta_k^2}{12} $$计算量化结果做无损压缩后的比特数:
$$ H(Q(x)) = -\sum_k P_k \log P_k = \underbrace{- \int_{-\infty}^{\infty}p_x(x)\log p_x(x) \mathrm dx }_{h(X)} + \log \frac{1}{\Delta} $$由 $\Delta = \sqrt{12\sigma_{qn}^2} = 2\sigma_{qn}\sqrt{3}$ ,
$$ H(x) = h(x) + \log \frac{1}{2\sigma_{qn}\sqrt{3}} $$无损压缩的 bit 数为: $\tilde{R} = h(X) - \frac{1}{2}\log \sigma_{qn}^2 - 1.8$
对于均匀量化:
$$ \Delta_k = \frac{x_{max} - x_{min}}{L} = \frac{2x_{max}}{L}, \forall k $$于是
$$ \sigma_{qn}^2 = \frac{\Delta^2}{12} = \frac{x_{max}^2}{3L^2} $$这里的 $\sigma_{qn}^2$ 是正常量化噪声,仅仅是计算了信号落在 $[-x_{max}, x_{max}]$ 内的情况
如果信号落在 $[-x_{max}, x_{max}]$ 以外,就就近判断至两端的量化区间,产生过载噪声
$$ \sigma_{qo}^2 = \int_{x_{max}}^{\infty}(x - x_{max})^2p_x(x)\mathrm dx + \int^{-x_{max}}_{-\infty}(x + x_{max})^2p_x(x)\mathrm dx = 2\int_{x_{max}}^{\infty}(x - x_{max})^2p_x(x)\mathrm dx $$总噪声等于正常量化噪声加上过载噪声:
$$ \sigma_{qs}^2 = \sigma_{qn}^2 + \sigma_{qo}^2 $$如果用 $R$ bit 编码:
$$ \Delta_k = \frac{2x_{max}}{L} = \frac{x_{max}}{2^{R - 1}}\\ \sigma_{qn}^2 = \frac{\Delta^2}{12}\int_{-x_{max}}^{x_{max}}p_x(x)\mathrm dx = \frac{x_{max}^2}{3 \times 2^{2R}}\int_{-x_{max}}^{x_{max}}p_x(x)\mathrm dx $$定义非过载信号功率:
$$ \sigma_s^2 = \int_{-x_{max}}^{x_{max}}x^2p_x(x)\mathrm dx $$当 $\int_{-x_{max}}^{x_{max}}p_x(x)\mathrm dx \rightarrow 1$ , $SNR_q \approx \frac{\sigma_s^2}{x_{max}^2/(3 \times 2^{2R})} = 3 \times 2^{2R} \times \zeta^2$ ,这里定义 $\zeta = \frac{\sigma_s}{x_{max}}$ 为量化范围内信号的饱满程度。
对数单位下:
$$ SNR_q(dB) = 6.02R + 20\log_{10}(\zeta) + 4.77 $$- 多一个 bit, $SNR_q$ 提升 $6.02dB$
- $\zeta$ 要在合理范围, $\zeta$ 过大时过载会严重劣化性能
最优量化
目标:给定量化区间总数,最小化量化噪声
优化问题:
$$ \min \sum\limits_{k=1}^{L}\int_{x_k}^{x_{k + 1}}(x - y_k)^2 p_x(x)\mathrm dx\\ s.t. x_1\le y_1 \le x_2 \le y_2 \le \dots \le y_L \le x_{L + 1} $$分层电平在重建电平的中点:
$$ \frac{\partial \sigma_q^2}{\partial x_k} = 0\\ \Rightarrow x_{k, opt} = \frac{1}{2}(y_{k, opt} + y_{k - 1, opt}) $$重建电平在量化区间的质心:
$$ \frac{\partial \sigma_q^2}{\partial y_k} = 0\\ \Rightarrow y_{k, opt} = \frac{\int_{x_{k, opt}}^{x_{k+1, opt}}xp(x)\mathrm dx}{\int_{x_{k, opt}}^{x_{k+1, opt}}p(x)\mathrm dx} $$对于均匀分布,质心即中点(对于可导的概率分布,当分层很密的时候同样成立)
$$ y_{k, opt} = \frac{\int_{x_{k, opt}}^{x_{k+1, opt}}xp(x)\mathrm dx}{\int_{x_{k, opt}}^{x_{k+1, opt}}p(x)\mathrm dx} = \frac{1}{2}(x_{k, opt} + x_{k + 1, opt}) $$结合
$$ x_{k, opt} = \frac{1}{2}(y_{k, opt} + y_{k - 1, opt}) $$可得均匀分布的最佳量化是区间等分,中点重建
工程用量化
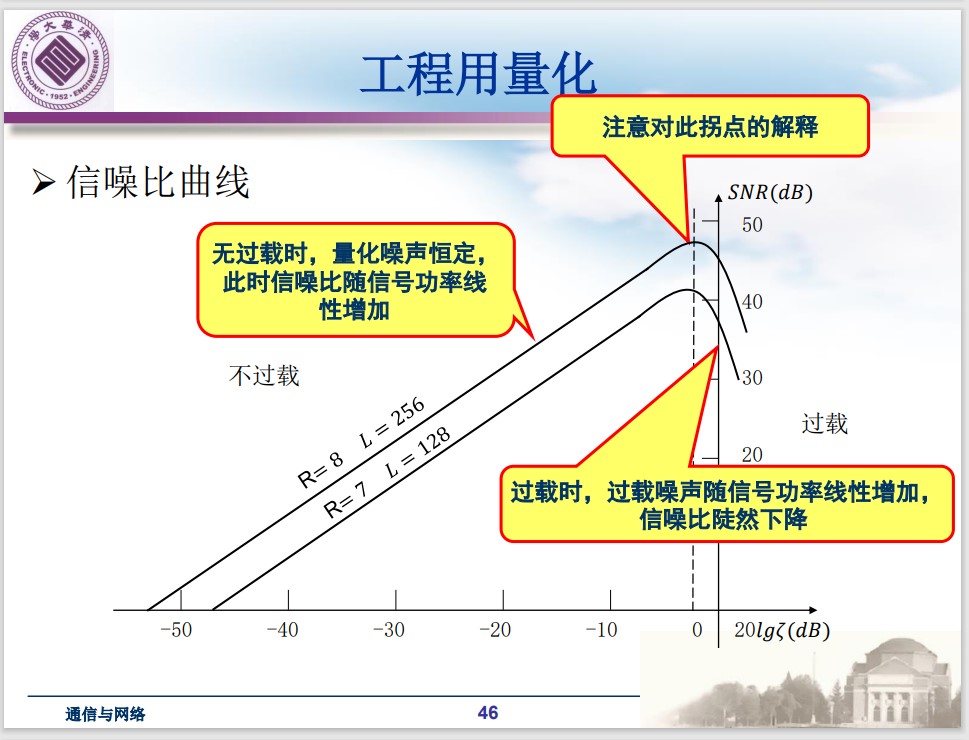
语音信号的量化
$[-V, V]$ 内均匀量化的缺陷:- 最适合 $[-V, V]$ 之间的有限分布
- 语音信号呈拉普拉斯分布,特点是:
- 信号功率小
- 动态范围大(长拖尾)
- 如果采用均匀量化
- 较大的V:增大[-V,V]内的量化噪声
- 较小的V:增大过载噪声
解决思路1:非均匀量化
语音信号的非均匀量化
均匀量化的问题
- 对具有不同“概率权重”的区间“一视同仁”
- 没有考虑概率密度对于量化噪声的影响
解决方案
- 对于信号经常出现的区域,使用较细的颗粒度进行量化
- 信号经常落入这个区域,减小该区域的量化噪声损失
- 对于信号不经常出现的区域,使用较粗的颗粒度进行量化
- 信号不经常落入这个区域,量化噪声稍大不会影响大局
采用取对数后均匀量化的方法:
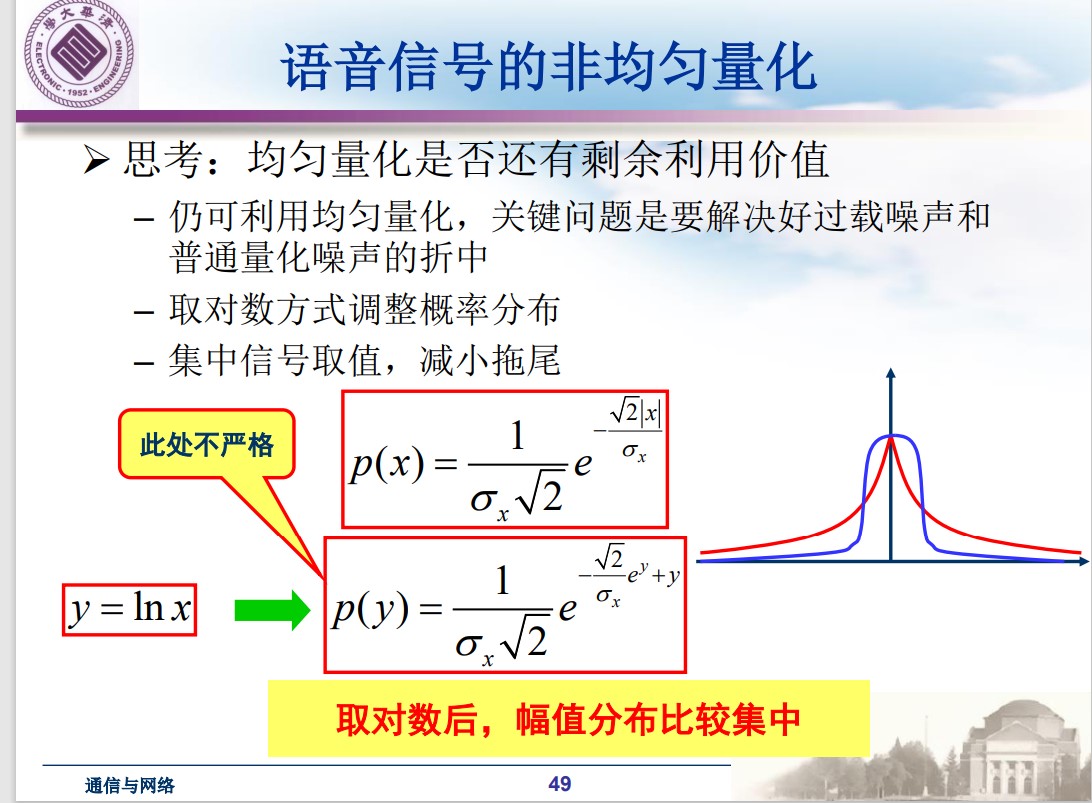
语音信号的瞬时压扩:
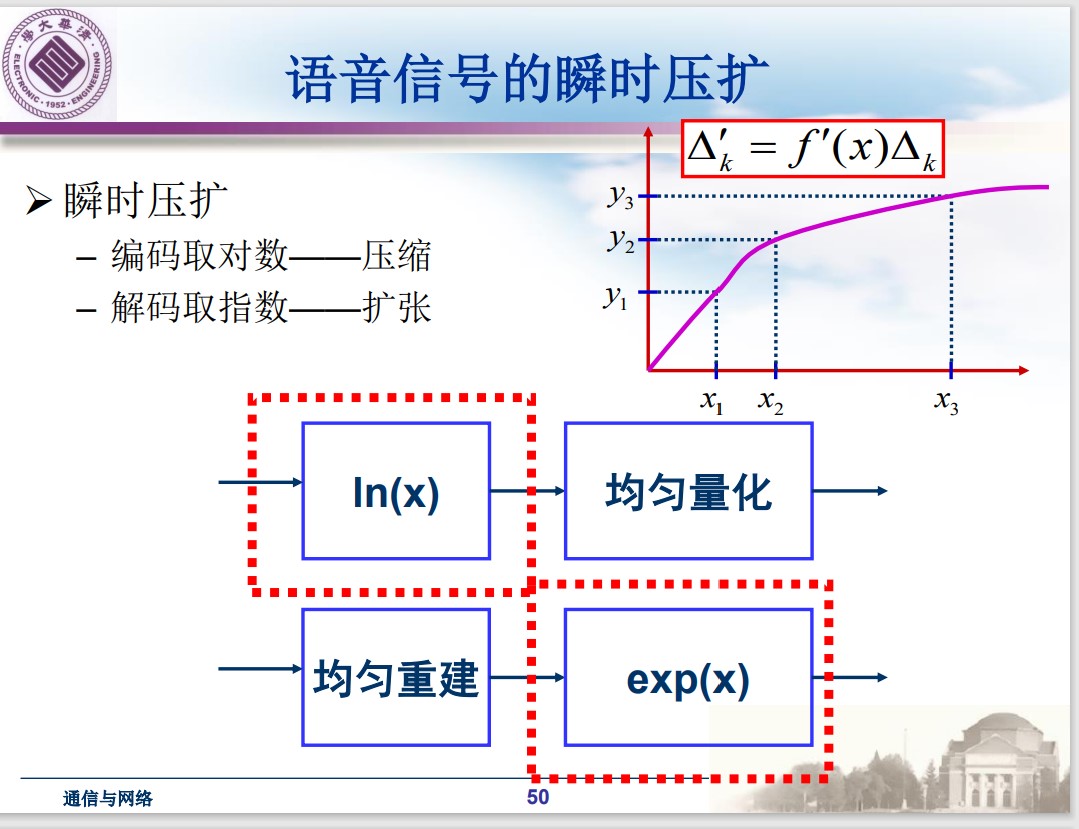
对数量化
- 正常量化信噪比与信号的分布无关
- 过载导致的噪声与信号的分布有关!
记 $\Delta_k$ 为对数化之前的量化区间, $\Delta_k^\prime = \Delta$ 为对数化之后的量化区间
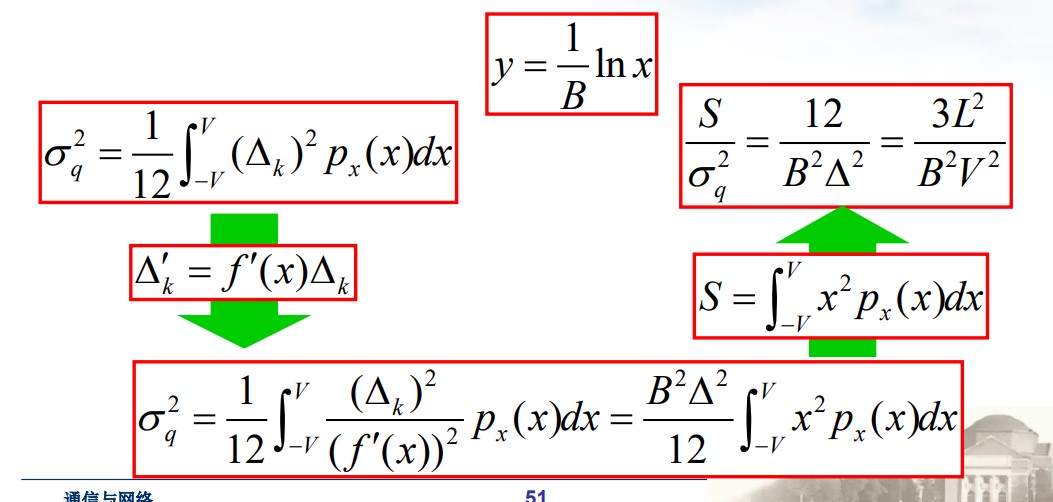
实用的对数量化
实际工程中,采用另外两个函数(线性放缩,更容易实现):
- A律(欧洲提出,我国采用)
ITU G.712建议中取A=87.6
小信号时,信噪比增加了24dB
μ律(美国提出)
- ITU G.712建议中取μ=255
- 小信号时,信噪比增加了33.5dB
脉冲编码调制(PCM)
- 语音信号的实际压缩编码方式
- 包括两个主要步骤
- 抽样: $f_s = 8000Hz$
- 量化与编码:使用近似对数压扩,每个抽样量化为8位
- PCM的输出码率为64kbps
该码率与其推导过程十分重要
PCM编码协议
基本思想
- 用13折线近似A律
- 用15折线近似μ律
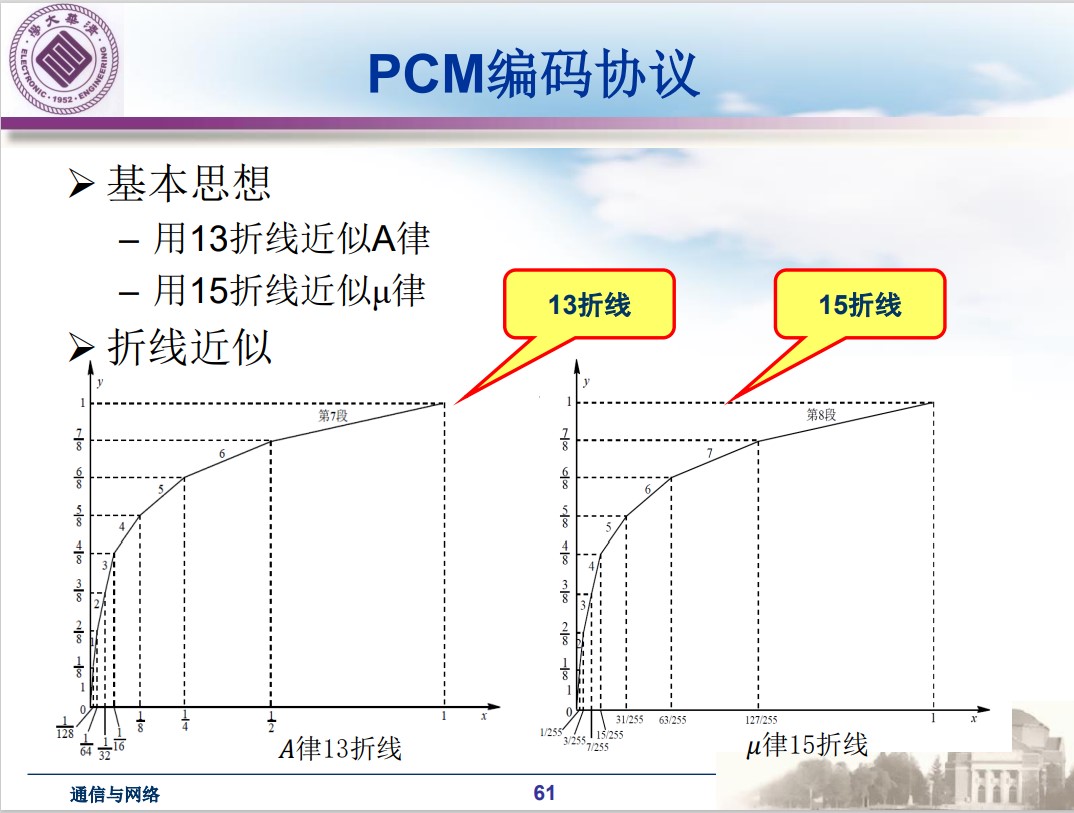
码字结构:
$$ \mathop{M_1}\limits_{极性码} \quad \underbrace{M_2 \quad M_3 \quad M_4}_{段落码}\quad \underbrace{M_5 \quad M_6\quad M_7 \quad M_8}_{电平码} \quad $$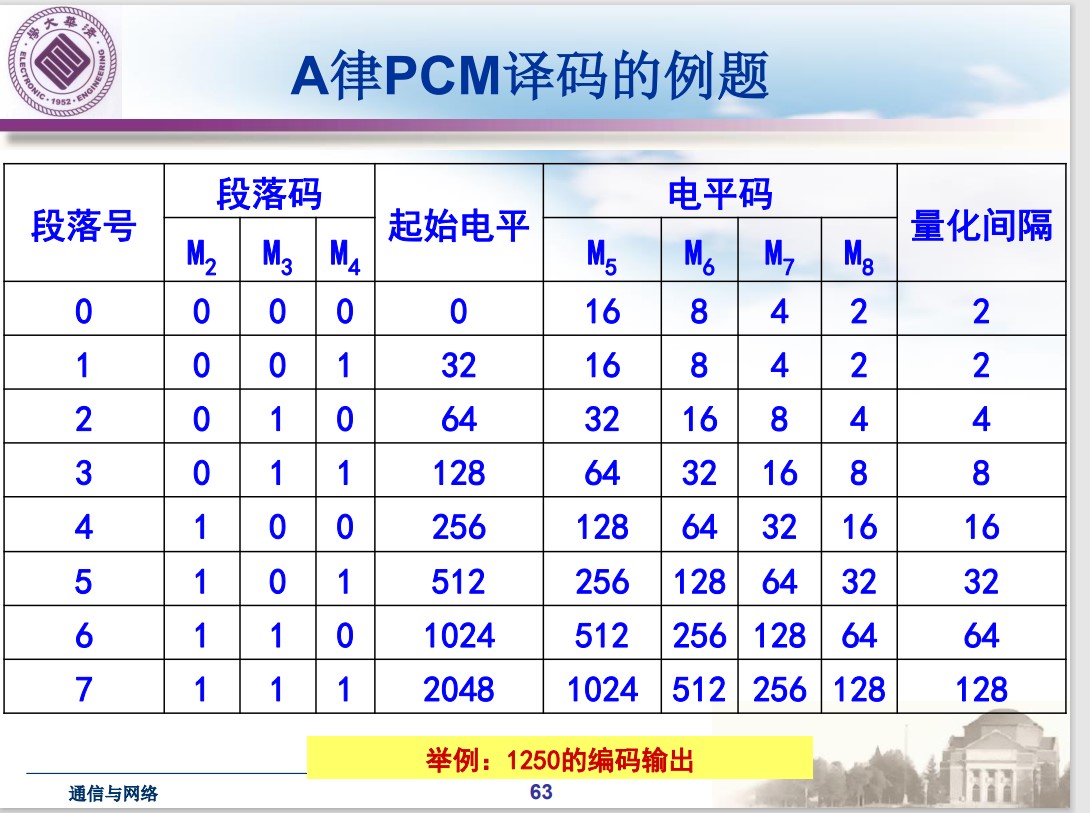
例:
1250的输出:1 110 0011
接收端解码: 1024 + 128 + 64 + 32 = 1248
数字基带传输
符号映射
符号集合
$M = |\mathcal{A}|$ 为符号集合 $\mathcal{A}$ 的符号数量。bit 承载量
每个符号最多可对应 $r = \log_2|\mathcal{A}|$ 个 bit,称为集合的 bit 承载量
数字通信的典型符号:
- ASK
- PAM
- PSK
- QAM
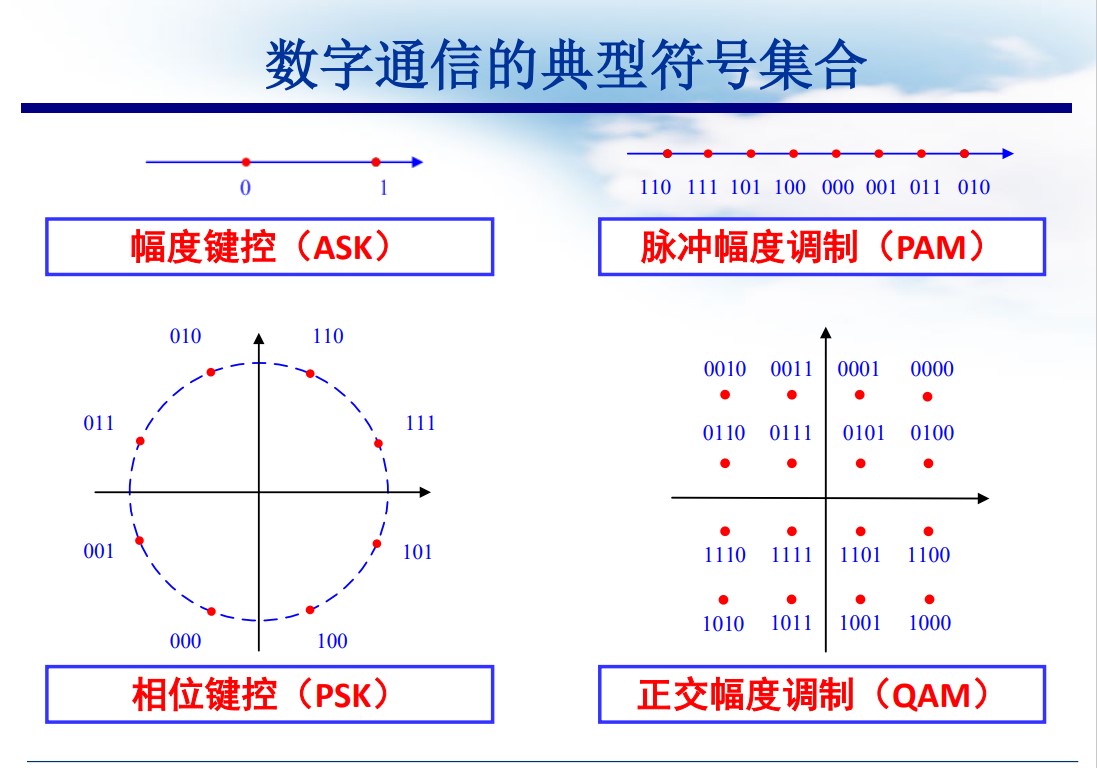
邻位最小差错映射:Grey 码
相邻符号对应的 bit 串仅有一位差异
符号周期(Symbol Period)
- 传输一个符号所需的平均时间
- $T_s$
通信速率:
- 符号速率: $R_s = \frac{1}{T_s}$
- Bit 速率: $R_b = R_s \log_2 M = \frac{1}{T_s}\log_2 M$
数字调制
基带调制:将时间上离散的符号,加载到时间上形成连续的波形
通信信号具有带宽受限特性,因为:
- 自然原因:各类通信线路,如双绞线,同轴电缆,射频功放等均对通过的频率有一定限制
- 人为原因:多用户频谱共享通信,如蜂窝无线系统,需约束每路信号的带宽,以免相互干扰
如何产生带限信号?
产生一个信号 $s(t) =\sum\limits_{k=-\infty}^{\infty}a_kg(t- k T_s)$ , $g(t) = \frac{\sin 2\pi Wt}{2\pi Wt}$ 是个带限信号。
$$ G(f) = \begin{cases} 1, |f| \le W,\\ 0, |f| \gt W \end{cases} $$让间隔 $T_s$ 的冲击 $a_k\delta(t - kT_s)$ 依次通过冲击响应为 $g(t)$ 的低通滤波器
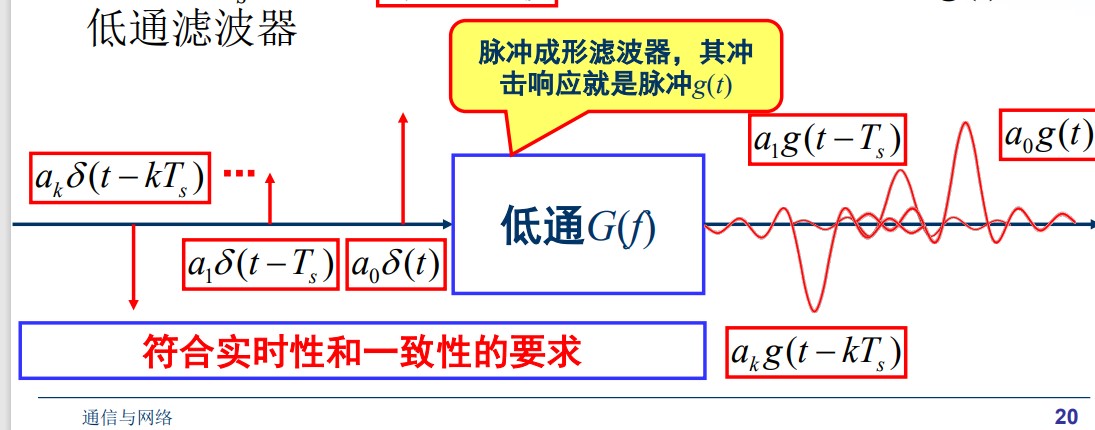
Nyquist 准则:无ISI条件
符号间串扰(Inter Symbol Interference, ISI)
对 $s(t)$ 采样:
$$ s(nT_s) = a_ng(0) + \underbrace{\sum\limits_{k=-\infty, k\ne n}^{\infty}a_kg\big((n - k)T_s\big)}_{\text{ISI}} $$怎么让 ISI 为0?
眼图:观察符号间串扰
眼图(Eye Pattern)是直观察看数字基带传输性能的有效方法,用一个示波器
$$ 垂直输入 \xrightarrow{接} 匹配滤波器的输出\\ 水平扫描速度 \xrightarrow{设为} 𝑅_𝑠的整数倍 $$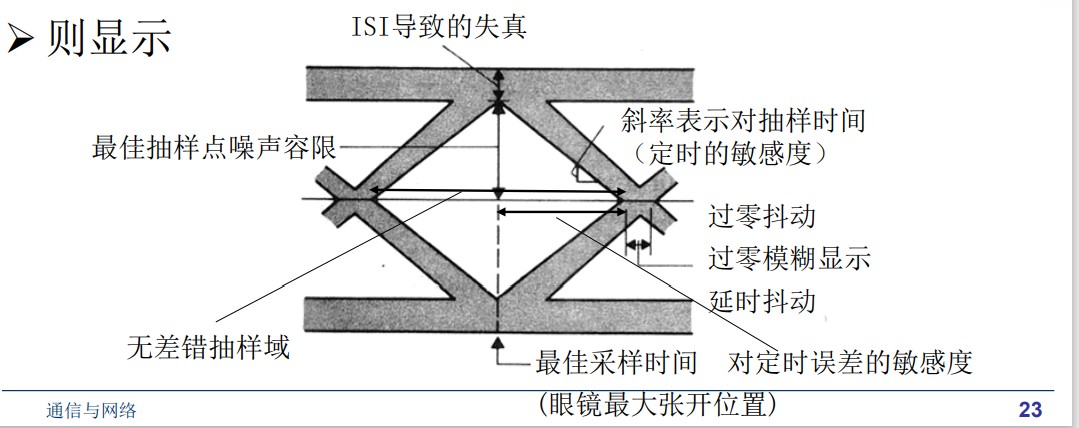
眼皮的厚度表示 ISI 的失真,眼睛的张开程度表示噪声容限。
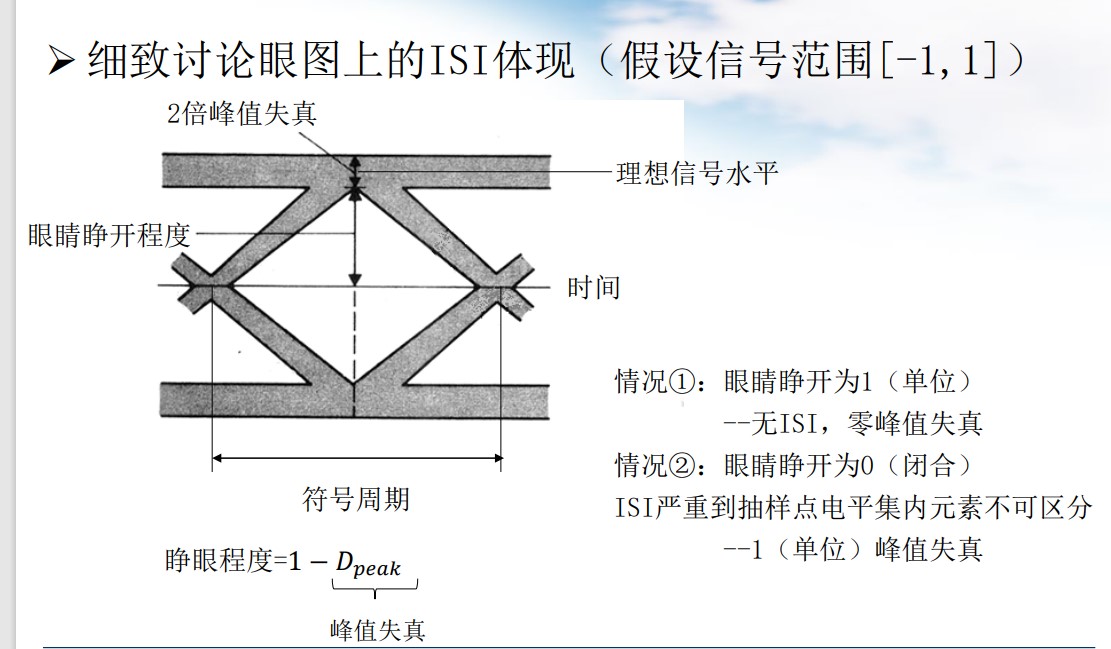
消除 ISI 对带限脉冲的要求
时域特征:
$$ \left.\begin{align*} g(0) &= 1\\ \sum\limits_{k=-\infty, k\ne n}^{\infty}a_kg\big((n - k)T_s\big) &= 0 \end{align*}\right\rbrace \Leftrightarrow \sum\limits_{k=-\infty, k\ne n}^{\infty}a_{n - k}g\big(kT_s\big) = 0\\ \Leftrightarrow g(kT_s) = \begin{cases} 1, k = 0,\\ 0, k \ne 0 \end{cases} \\ \lrArr g(t)\sum\limits_{n=-\infty}^{\infty}\delta(t + nT_s) = \delta(t) $$从频域提取特征:
$$ g(t)\sum\limits_{n=-\infty}^{\infty}\delta(t + nT_s) = \delta(t) \lrArr G(f) *\sum\limits_{n=-\infty}^{\infty}\frac{1}{T_s}\delta(f + \frac{n}{T_s}) = 1\\ \lrArr \sum\limits_{n=-\infty}^{\infty}G\left(f + \frac{n}{T_s}\right) = T_s $$Nyquist 准则
将带限脉冲的频谱分别平移 $n/T_s$ ( $n$ 为任意整数)若其叠加的结果对任意频率恒为定值,则 ISI 为0
通信速率与带宽效率
理解 Nyquist 准则
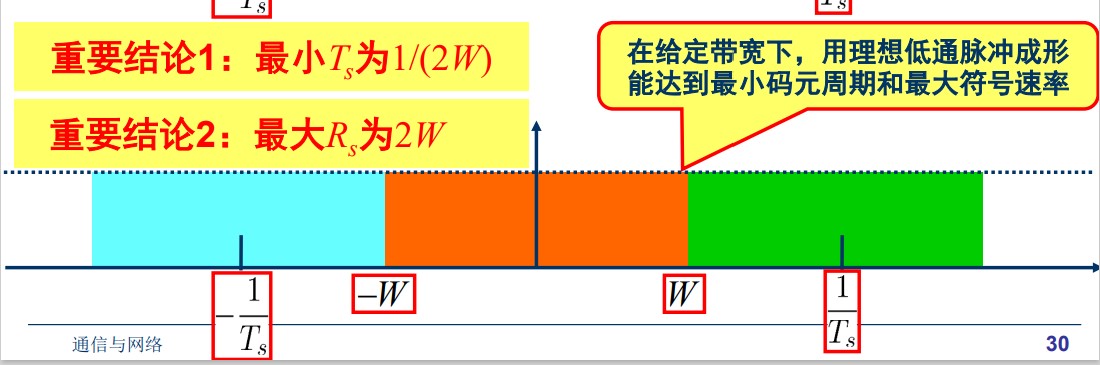
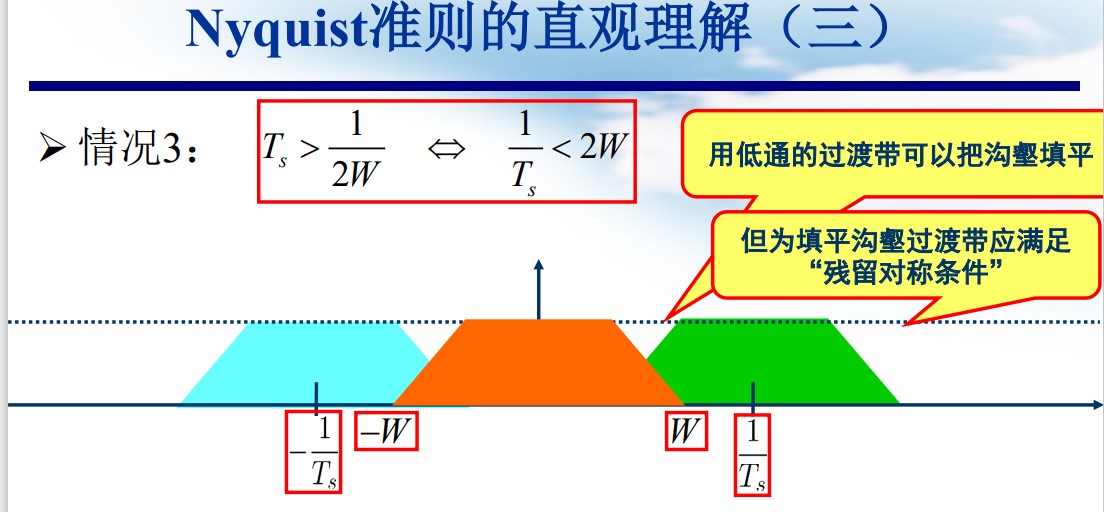
- 最大符号速率受制于带宽 $R_s = \frac{1}{T_s} \le 2W$
- 低通发送滤波器应该满足残留对称条件
通信速率与带宽效率
$$ R_s \le 2W\\ R_b = R_s \log_2 M\\ \Rightarrow R_b \le 2W \log_2 M $$- 针对给定形式的低通滤波器,可写出 $R_s$ 与 $W$ 之间的线性函数关系
信号功率与带宽效率
设单个符号的能量为 $E_s$
则信号功率为单位时间内的能量
$$ P = \frac{E_s}{T_s} = E_sR_s $$无冗余编码时,一个比特的能量为 $𝐸_𝑏$ ,则
$$ P = \frac{E_b\log_2 M}{T_s} = E_bR_b $$带宽效率的定义:单位带宽承载的速率
$$ \eta = \frac{R_b}{W} \le 2\log_2 M $$- 为什么不能无限制扩大符号集合?
过大的符号集合对信噪比有更高的要求,噪声容易干扰符号的分辨
升余弦滤波器
升余弦滤波器
由于理想滤波器难以实现,所以常用满足残留对称条件的非理想低通生成基带脉冲,最常用的就是升余弦滤波器
Raised Cosine(要记住)
$$ H(f) = \begin{cases} T_s, &0 \le |f| \lt \frac{1 - \alpha}{2 T_s}\\ \frac{T_s}{2}\left\lbrace1 + \cos \left[\frac{\pi T_s}{\alpha}\left(|f| - \frac{1 - \alpha}{2T_s}\right)\right]\right\rbrace, &\frac{1 - \alpha}{2 T_s} \le |f| \le \frac{1 + \alpha}{2 T_s}\\ 0, & |f| \gt \frac{1 + \alpha}{2 T_s} \end{cases} $$ $\alpha = 2WT_s - 1 \in [0, 1]$ 称为滚降系数,越小坡越陡,越大坡越缓。时域冲激响应:
$$ h(t) = \text{Sa}(\pi t/ T_s)\frac{\cos (\alpha\pi t/ T_s)}{1 - 4(\alpha t/T_s)^2} $$升余弦滤波器的性质:
常考性质:
$$ W = \frac{\alpha + 1}{2T_s} = \frac{\alpha + 1}{2}R_s \Rightarrow R_s/2 \le W \le R_s\\ R_s = \frac{1}{T_s} = \frac{2}{\alpha + 1} W \Rightarrow W \le R_s \le 2W $$带宽效率
$$ \eta_b = \frac{R_s\log_2|\mathcal{S}|}{W} \le 2\log_2|\mathcal S| $$升余弦滤波器的带宽效率
$$ \eta_b = \frac{2\log_2|\mathcal{S}|}{\alpha + 1} $$PCM 语言信号速率 64kbps:8 bit 采样,8 bit 量化,8*8 = 64.
例题一:传送一路PCM语音信号
- 若带宽限制为40kHz,采用二元码,则可用滚降系数范围
是多少? - 若采用四元码,最多需要多少带宽?
解:PCM语音信号是64kbps
- 采用二元码,则所需符号速率为 $R_s = R_b = 64kbps$
则 $\frac{\alpha + 1}{2}64 \le 40$ , $0\le \alpha \le 0.25$
采用四元码: $R_s = \frac{R_b}{\log_24} = 32kbps$
- $W \le R_s = 32kHz$
例题二:若传送一路信号 $𝑅_𝑏$ = 112kbps,信道带宽𝑊 = 30𝑘bps,
求𝑀和𝛼
认定 $\log_2M = k$ 为整数,则 $k = 2 或 3$ 。对应可解:
$$ \alpha_1 = \frac{1}{14}, M_1 = 4\\ \alpha_2 = \frac{17}{28}, M_2 = 8 $$通信信号的功率谱计算
功率谱刻画了随机过程的功率在频域上的分布。
- 对于宽平稳过程(自相关只与时差有关),功率谱易于从 $R(\tau)$ 的傅里叶变换得到,即 $S(f) = \mathcal{F}[R(\tau)]$
- 但是,通信信号一般不是宽平稳过程,而是周期平稳过程: $R(t_1, t_2) = R(t_1 + kT_s, t_2 + kT_s)$
定义
$$ \overline{R}(\tau) = \frac{1}{T_s} \int_{0}^{T_s}R(t+\tau, t)\mathrm dt $$则其功率谱
$$ S(f) = \mathcal{F}[\overline{R}(\tau)] $$若输入信号的功率谱 $S_{AI}(f)$ ,输出为 $S_A(f)$ ,则对于宽平稳和周期平稳信号均有卷积关系:
$$ S_A(f) = S_{AI}(f)|H(f)|^2 $$证明可以采用样本统计法:假设符号序列的长度为 $2N - 1$ .
$$ s_{AI}(t) =\sum\limits_{k=-N}^{N}a_k\delta(t - k T_s)\\ s_{A}(t) =\sum\limits_{k=-N}^{N}a_kh(t - k T_s)\\ \hat s_{AI}(f) =\sum\limits_{k=-N}^{N}\exp(-j2k\pi T_sf)\\ \hat s_{A}(f) = H(f)\sum\limits_{k=-N}^{N}\exp(-j2k\pi T_sf) $$功率谱的定义:
$$ S(f) = \lim\limits_{N\rightarrow\infty} \frac{E(|\hat s(f)|^2)}{(2N + 1)T_s} $$可以验证 $S_A(f) = S_{AI}(f)|H(f)|^2$
针对样本统计法,可以算出 $E(|\cdot|^2)$ 的表达式:
$$ S_A(f) = \frac{|H(f)|^2}{T_s}\sum\limits_{n=-\infty}^{\infty}R_a[n] \exp (-j2n\pi T_s f) $$这里 $R_a[m]$ 是输入符号的自相关。
先考虑无记忆调制,符号之间相互独立:
$$ R_a[n] = E[a_ia_{i+n}] = \begin{cases} \sigma_a^2+m_a^2 &n=0\\ m_a^2 &n\ne 0 \end{cases} $$其中, $m_a = E[a_n]$ , $\sigma_a^2 = E[a_n^2] - m_a^2$
于是,重写累加部分:
$$ \begin{align*} &\sum\limits_{n=-\infty}^{\infty}R_a[n] \exp (-j2n\pi T_s f) \\ =& \sigma_a^2 + m_a^2\sum\limits_{n=-\infty}^{\infty}\exp\big[-jn(2\pi T_s)f\big]\\ =& \sigma_a^2 + \frac{1}{T_s}\sum\limits_{n=-\infty}^{\infty}\delta\bigg(f - \frac{n}{T_s}\bigg) \end{align*} $$从而
$$ S_A(f) = \underbrace{\frac{\sigma_a^2}{T_s}|H(f)|^2}_{连续谱} + \underbrace{\frac{m_a^2}{T_s^2}\sum\limits_{n=-\infty}^{\infty}\bigg|H\bigg(\frac{n}{T_s}\bigg)\bigg|^2 \delta\bigg(f - \frac{n}{T_s}\bigg)}_{线谱} $$此式应用的两个条件:
- 无记忆
- 不同符号波形一致
线谱:可用于定时恢复。方便恢复时钟分量。
任意波形调制
之前将 $a_i$ 映射为 $a_ih(t)$ ,可以推广:
$$ \forall a_i \ne a_j, s_i(t) \ne s_j(t) $$有时候由于信号功率需要保持稳定(恒包络调制),对不同符号采用不同波形,而不是采用变化幅度的信号。
若任意波形二元调制信号 $s(t) =\sum\limits_{k=-\infty}^{\infty}g_k(t)$
$$ g_k(t) = \begin{cases} s_1(t - kT_s), w.p.\ p\\ s_2(t - kT_s), w.p.\ \bar p = 1 - p \end{cases} $$(w. p. = with probability)
分解为直流分量和交流分量:
$$ s(t) = \underbrace{E(s(t))}_{DC,记为v(t)} + \underbrace{s(t) - E(s(t))}_{AC, 记q(t)} $$则
$$ v(t) = \sum\limits_{k=-\infty}^{\infty}[ps_1(t - kT_s) + \bar p s_2(t - kT_s)] $$这是一个周期为 $𝑇_𝑠$ 的确定性周期信号,功率谱由傅里叶展开计算
$$ S_v(f) =\sum\limits_{n=-\infty}^{\infty}|D_n|^2\delta(f - \frac{n}{T_s})\\ D_n = \frac{1}{T_s}\int_{-T_s/2}^{T_s/2}v(t)e^{-j2\pi t/T_s}\mathrm dt = \frac{1}{T_s}\Big(p\hat s_1\big(\frac{n}{T_s}\big) + \bar p \hat s_2(\frac{n}{T_s}\big)\Big) $$ $$ S_v(f) = \frac{1}{T_s}\sum\limits_{n=-\infty}^{\infty}\bigg|\Big(p\hat s_1\big(\frac{n}{T_s}\big) + \bar p \hat s_2(\frac{n}{T_s}\big)\Big)\bigg|^2 \delta(f - \frac{n}{T_s}) $$用样本统计法计算 $S_q(f)$ :
$$ \begin{align*} S_q(f) =& \lim\limits_{N\rightarrow\infty} \frac{E(|\hat q_N(f)|^2)}{(2N + 1)T_s}\\ =& \frac{p\bar p}{T_s}|\hat s_1 (f) - \hat s_2(f)|^2 \end{align*} $$ $$ S(f) = \frac{p\bar p}{T_s}|\hat s_1 (f) - \hat s_2(f)|^2 + \frac{1}{T_s}\sum\limits_{n=-\infty}^{\infty}\bigg|\Big(p\hat s_1\big(\frac{n}{T_s}\big) + \bar p \hat s_2(\frac{n}{T_s}\big)\Big)\bigg|^2 \delta(f - \frac{n}{T_s}) $$基带解调
最佳接收用于在给定发送功率下提高信噪比
最佳判决用于在给定信噪比下降低误码率
基带传输的噪声模型
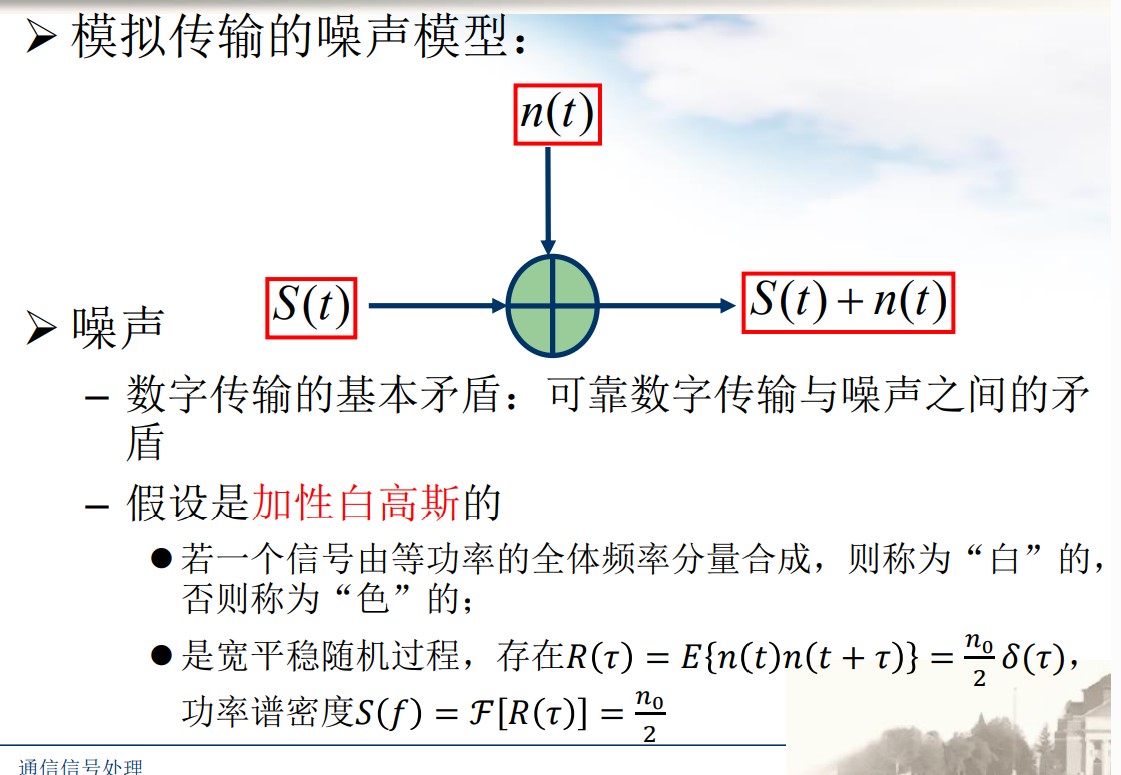
如何选择解调方案?
方案一:直接抽样
在信号的峰值位置 $t = kT_s$ 抽样最好。
但噪声方差满足:
$$ \sigma^2 = E \lbrace n^2(t_1) \rbrace = R(0) = \frac{n_0}{2}\delta(0) \rightarrow \infty $$(理想的白噪声信号具有无穷大功率)
真实的噪声环境下,接收信号质量随着噪声信号功率的增加而变差。如果信号的峰值处恰好噪声很大,则产生严重失真。
方案二:能量累积
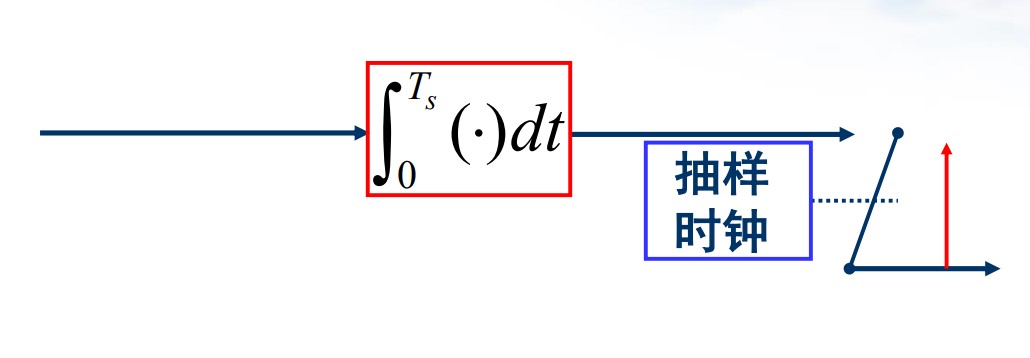
噪声信号仍为高斯随机变量:
$$ n = \int_{0}^{T_s}n(t)\mathrm dt $$噪声方差:
$$ \sigma^2 = E\lbrace n^2 \rbrace = \int_{0}^{T_s}\int_{0}^{T_s}\frac{n_0}{2}\delta(t_1 - t_2)\mathrm dt_1\mathrm dt_2 = \frac{n_0T_s}{2} $$信噪比:
$$ \frac{S}{N} = \frac{\left (\int_{0}^{T_s}a_i h(t)\mathrm dt \right)^2}{T_sn_0/2} $$直接积分不是最好的方案。
方案三:匹配滤波
匹配滤波的基本思想就是对接收值进行加权线性累加,从而最大化抽样时刻信号功率与噪声功率的比值。
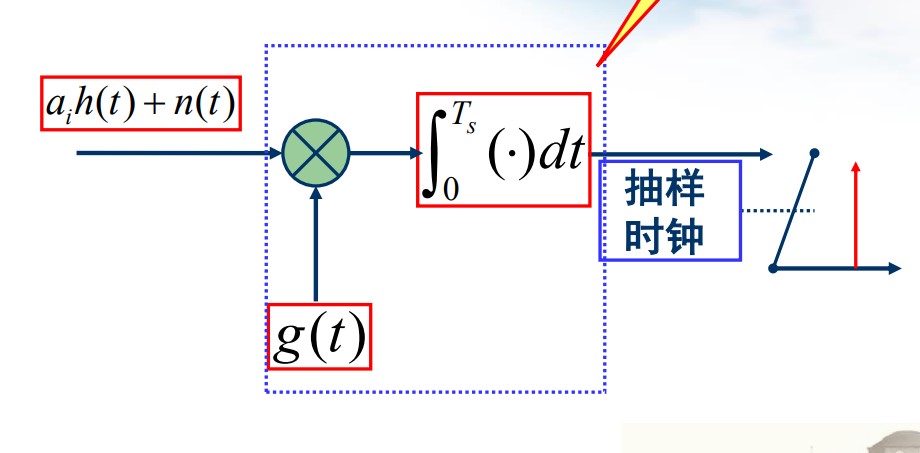
相关器为 $g(t)$ 。假设信号为实信号。复信号有类似结论。
$$ P_S = \left |\int_{0}^{T_s}a_ih(t)g(t)\mathrm dt \right|^2\\ P_N = \mathbf E \left [ \left | \int_{0}^{T_s}n(t)g(t)\mathrm dt \right|^2 \right] = \frac{1}{2}n_0 \int_{0}^{T_s}g^2(t)\mathrm dt $$利用 Cauchy-Schwartz 不等式:
$$ \frac{\left |\int_{0}^{T_s}a_ih(t)g(t)\mathrm dt \right|^2}{\frac{1}{2}n_0 \int_{0}^{T_s}g^2(t)\mathrm dt} \le \frac{2}{n_0}\int_{0}^{T_s}a_i^2h^2(t)\mathrm dt $$等号成立当且仅当 $g(t) = kh(t)$ 。
若为复信号,则需要
$$ g(t) = h^*(t) $$如何把相关器写成滤波器形式?
(滤波=卷积,相关和卷积就是差一个反褶的关系)
$$ y(t) = [a_ih(t) + n(t)] * h_m(t) = \int_{-\infty}^{\infty}[a_ih(\tau) + n(\tau)]h_m(t - \tau)\mathrm d\tau $$考虑因果系统,一般将符号波形的最高点设置为 $t = T_s$ :
$$ y(T_s) = \int_{-\infty}^{\infty}[a_ih(\tau) + n(\tau)]h_m(T_s - \tau)\mathrm d\tau $$与相关器比较得到匹配滤波器的表达式:
$$ h_m(t) = h(T_s - t) $$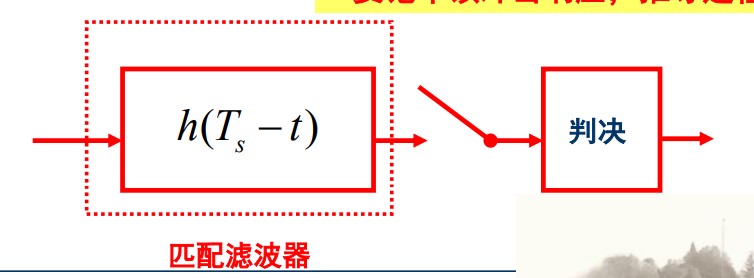
图中的“开关”是抽样。
匹配滤波的频域解释:
$$ P_S = \left | \int_{-\infty}^{\infty}H(f)H_m(f)e^{j2\pi fT_s}\mathrm df \right|^2\\ P_N = \frac{n_0}{2}\int_{-\infty}^{\infty}|H_m(f)|^2\mathrm df\\ \frac{S}{N} = \frac{\left | \int_{-\infty}^{\infty}H(f)H_m(f)e^{j2\pi fT_s}\mathrm df \right|^2}{\frac{n_0}{2}\int_{-\infty}^{\infty}|H_m(f)|^2\mathrm df} = \frac{2}{n_0}\int_{-\infty}^{\infty}|H(f)|^2\mathrm df $$Cauchy-Schwartz
$$ H_m(f) = H^*(f)e^{-j2\pi fT_s} $$匹配滤波的增益
数字传输的优势:数字传输中,基带脉冲h(t)是给定的,在整个码元周期内可以相干累加,而同时让噪声在整个周期内自我抵消
$$ \left (\frac{S}{N} \right)_{\text{match}} \bigg/ \left (\frac{S}{N} \right)_{\text{w.o.match}} = \frac{T_s \int_{0}^{T_s}h^2(t)\mathrm dt}{\left ( \int_{0}^{T_s}h(t)\mathrm dt \right)^2} \ge \frac{T_s \int_{0}^{T_s}h^2(t)\mathrm dt}{\int_{0}^{T_s}1\mathrm dt\int_{0}^{T_s}h^2(t)\mathrm dt} = 1 $$匹配滤波的信噪比
$$ \frac{S}{N} = E \left [ \frac{2}{n_0} \int_{0}^{T_s}a_i^2h^2(t)\mathrm dt \right] = \frac{\int_{0}^{T_s}E[a_i^2]h^2(t)\mathrm dt}{n_0/2} = \frac{E_s}{n_0 / 2} $$分子——传送一个符号的能量
分母——噪声谱密度,单位是能量的单位
以上采用的是等效基带模型。采用实际物理波形模型:
$$ S = \frac{E_s}{T_s} = E_sR_s\\ N = Wn_0\\ \frac{S}{N} = \frac{E_s}{n_0}\frac{R_s}{W}\\ $$两个模型推得的信噪比表达式不同,差异在于等效基带模型使用了匹配滤波器,获得了最优的信噪比:
$$ \frac{R_s}{W} \le 2 \Rightarrow\left (\frac{S}{N} \right)_{\text{max}} = \frac{E_s}{n_0/2} $$从实际物理波形模型来看,上式取等的条件应该是基带脉冲采用的是理想低通(Sa 函数),如果用升余弦滤波
$$ \frac{R_s}{W} = \frac{2}{\alpha + 1} \Rightarrow \left(\frac{S}{N}\right)_{\text{max}} = \frac{E_s}{n_0/2}\frac{2}{\alpha + 1} $$但是,在等效基带模型中,我们考虑的是任意脉冲 $h(t)$ ,并没有要求它的形状,这两个模型在最优信噪比的产生条件上出现了矛盾?
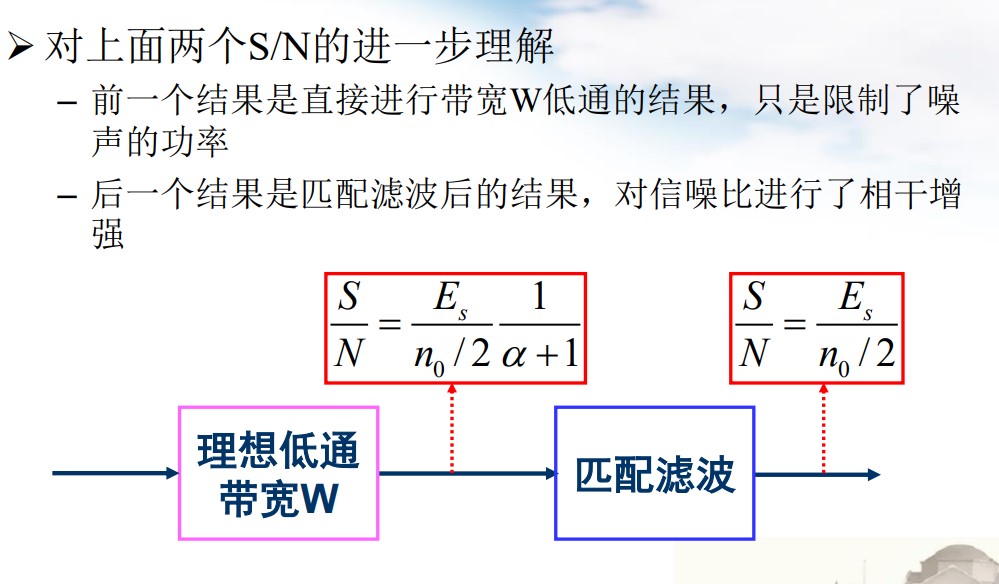

传送一串符号
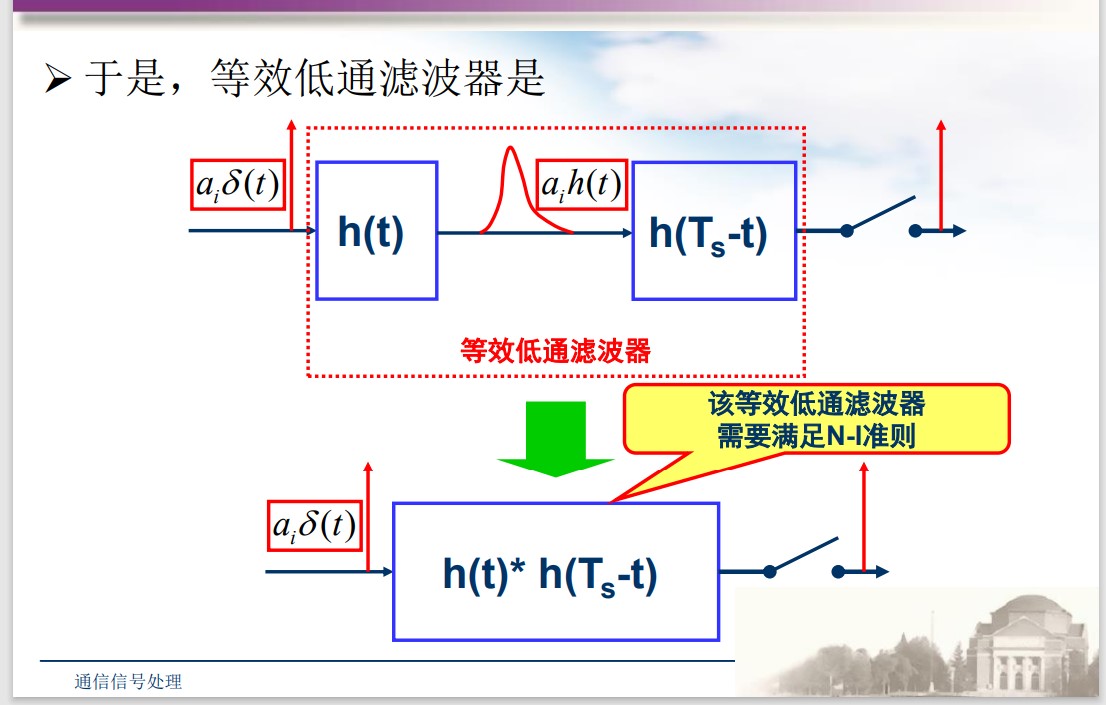
无 ISI 条件:
$$ h(t)*h_m(t) = h(t) * h(T_s - t)\\ H(f)H_m(f) = H(f)H^*(f)e^{-j2\pi fT_s} = \left | H(f) \right|^2 e^{-j2\pi fT_s} $$从而有根号奈奎斯特条件:
$$ H(f) = \sqrt{H_{N-I}(f)}e^{-j2\pi fT_s} H_m(f) = \sqrt{H_{N-I}^*(f)}e^{-j2\pi fT_s} $$这就要求发送和接受滤波器要满足如下要求:
$$ h_T(t) = h_{\sqrt{N}}\left ( t - \frac{T_s}{2} \right)\\ h_R(t) = h_{\sqrt{N}}\left (\frac{T_s}{2} - t\right) = h_T(T_s - t) $$符号差错模型:

判决与差错
最佳判决
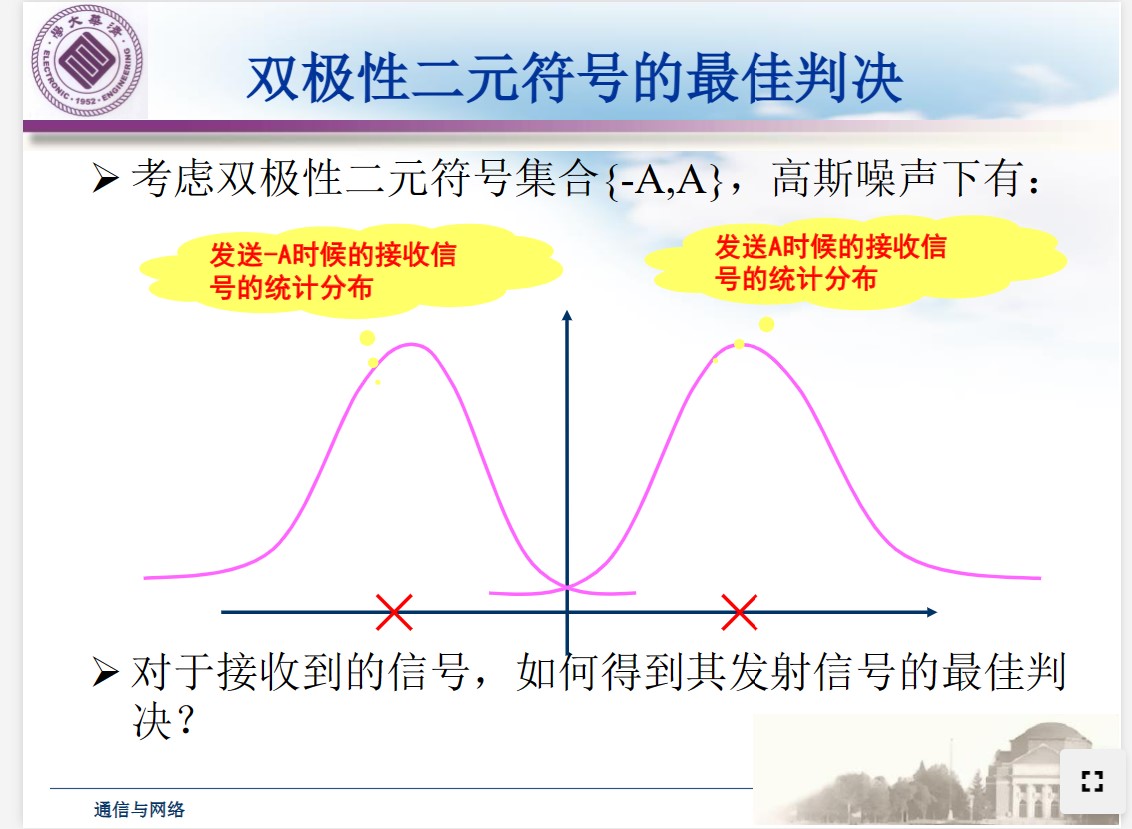


多元符号的最佳判决
$$ a^* = \argmax_{a\in U} f(y|a)f(a)\\ f(a) = \frac{1}{M}\\ a^* = \argmax_{a\in U} f(y|a)\\ $$ $y = a + n$ 的条件分布是 $$ f(y|a) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(y - a)^2}{2\sigma^2}\right) $$从而得到
$$ a^* = \argmin_{a\in U} |y - a| $$选择一个符号,让它到接收符号y距离最小,以此作为判决结果!
双极性码的判决门限:
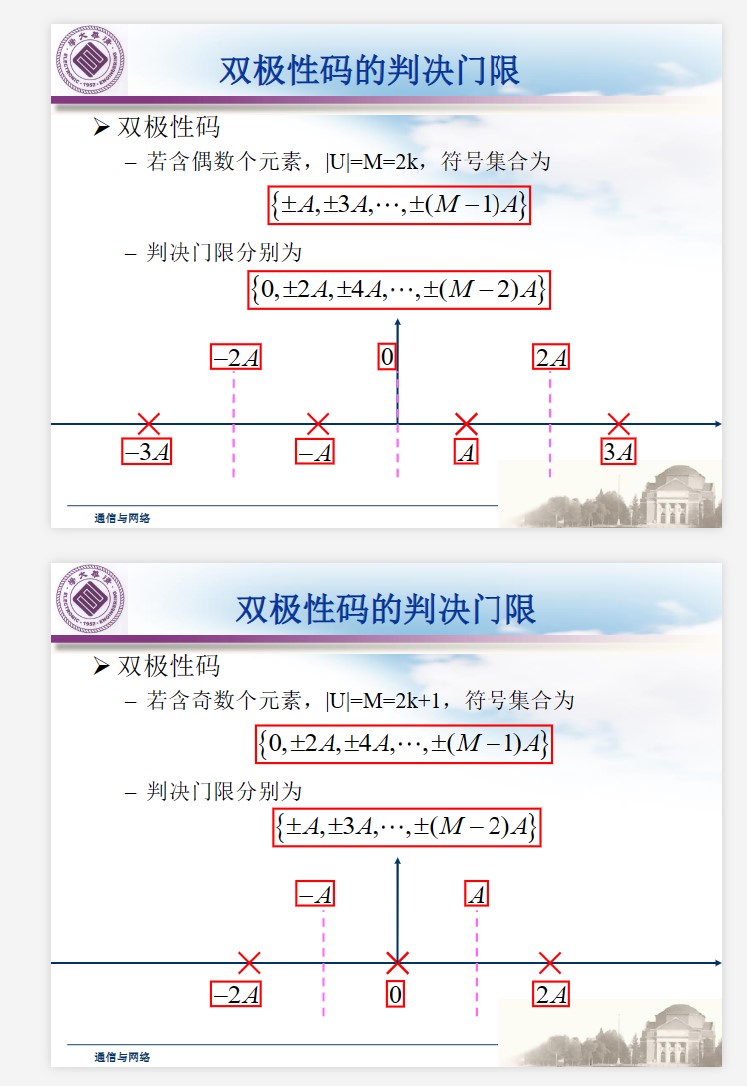
单极性码的判决门限:

SER & BER
考虑二元符号
发送 A 的出错概率:
$$ \int_{-\infty}^{0}f(y|a = A)\mathrm dy = \int_{A/\sigma}^{\infty}\frac{1}{\sqrt{2\pi}}\exp \left ( -\frac{t^2}{2} \right)\mathrm dt = Q \left ( \frac{A}{\sigma} \right) $$发送 -A 的出错概率:
$$ \int_{-\infty}^{0}f(y|a = A)\mathrm dy = Q \left ( \frac{A}{\sigma} \right) $$从而平均符号差错概率:
$$ P_s = \frac{1}{2}\left (Q \left ( \frac{A}{\sigma} \right) + Q \left ( \frac{A}{\sigma} \right) \right) = Q \left ( \frac{A}{\sigma} \right) $$称为符号差错概率(Symbor Error Probability, SEP),其统计结果称为误符号率(Symbol Error Ratio, SER)
由于Q是减函数,所以误符号率随A增大而减小,随噪声标准差增大而增大
误符号率不关心具体的A或标准差,而是由其比值所决定
对于多元而言:
对于任意符号集合,只要某判决门限与符号距离为A,则由于超出该判决门限而差错的条件概率就是:
$$ Q \left ( \frac{A}{\sigma} \right) $$计算信噪比:
信号平均功率: $S = \frac{1}{M}\sum\limits_{i=1}^{M}|a_i|^2$
信号峰值功率: $S_p = \max_{a_i \in U} |a_i|^2$
噪声功率: $N = \sigma^2$
对于双极性二元符号,平均功率为 $S = A^2$
从而信噪比为
$$ \frac{S}{N} = \frac{A^2}{\sigma^2} $$利用等效关系得到误符号率和信噪比的关系
$$ P_s = Q \left ( \frac{A}{\sigma} \right) = Q \left ( \sqrt{\frac{S}{N}} \right) $$更一般的二元码 SER
$$ U = \lbrace D-A, D+A \rbrace\\ \zeta = \frac{D}{A}\\ P_s = Q(\sqrt{\frac{S}{(1 + \zeta^2)N}}) $$更一般的 M 元码 SER
符号集合为 $\lbrace D - (M - 1)A, \dots, D + (M - 1)A \rbrace$
$$ \zeta = \frac{D}{A\sqrt{\frac{M^2 - 1}{3}}}\\ P_s = \frac{2(M - 1)}{M}Q \left ( \sqrt{\frac{3}{M^2 - 1}\frac{S}{(1 + \zeta^2)N}} \right) $$双极性 M 元码的 SER (掌握计算方法)
$$ P_s = \frac{2(M - 1)}{M } Q \left ( \sqrt{\frac{3}{M^2 - 1} \frac{S}{N}}\right) $$无论M为奇数还是偶数,结果都是一样的!
单极性 M 元码的 SER (掌握计算方法)
$$ P_s = \frac{2(M - 1)}{M } Q \left ( \sqrt{\frac{3}{2(M - 1)(2M - 1)} \frac{S}{N}}\right) $$要使得双极性和单极性码的 SER 相同,二者的信噪比的比值为
$$ \left ( \frac{S}{N} \right)_d \bigg / \left ( \frac{S}{N} \right)_s = \frac{M^2 - 1}{2(M - 1)(2M - 1)} \approx \frac{1}{4} $$显然,双极性的性能更好,它对信噪比的要求是单极性的四分之一,更能忍受噪声。
误比特率(Bit Error Rate, BER):
$$ P_b \approx \frac{P_s}{\log_2M} $$注意这是近似结果,且有成立条件,只对二元码是严格成立的!
- 假设一个符号的错判导致 1bit 的错误,假设成立的条件:
- Grey 码映射
- 信噪比不过于小
各类符号集合的 BER
双极性二元码
$$ P_b = Q \left ( \sqrt{\frac{S}{N}} \right) $$单极性二元码
$$ P_b = Q \left ( \sqrt{\frac{S}{2N}} \right) $$单极性二元码损失了 3 dB.
双极性 M 元码
$$ P_b = \frac{2(M - 1)}{M\log_2 M}Q(\sqrt{\frac{3}{M^2 - 1}\frac{S}{N}}) $$单极性 M 元码
$$ P_b = \frac{2(M - 1)}{M\log_2 M} Q \left ( \sqrt{\frac{3}{2(M - 1)(2M - 1)} \frac{S}{N}}\right) $$由于
$$ \frac{S}{N} = 2\log_2 M\frac{E_b}{n_0} $$故可以把 SER 和 BER 用 $E_b/n_0$ 表示:
双极性二元码:
$$ P_s = Q \left ( \sqrt{\frac{2E_b}{n_0}} \right)\\ P_b = Q \left ( \sqrt{\frac{2E_b}{n_0}} \right) $$单极性二元码:
$$ P_s = Q \left ( \sqrt{\frac{E_b}{n_0}} \right)\\ P_b = Q \left ( \sqrt{\frac{E_b}{n_0}} \right) $$双极性 M 元码:
$$ P_s = \frac{2(M - 1)}{M}Q(\sqrt{\frac{6\log_2 M}{M^2 - 1}\frac{E_b}{n_0}})\\ P_b = \frac{2(M - 1)}{M\log_2 M}Q(\sqrt{\frac{6\log_2 M}{M^2 - 1}\frac{E_b}{n_0}}) $$单极性 M 元码:
$$ P_s = \frac{2(M - 1)}{M} Q \left ( \sqrt{\frac{3\log_2 M}{(M - 1)(2M - 1)} \frac{E_b}{n_0}}\right)\\ P_b = \frac{2(M - 1)}{M\log_2 M} Q \left ( \sqrt{\frac{3\log_2 M}{(M - 1)(2M - 1)} \frac{E_b}{n_0}}\right) $$例子:相移键控 MPSK
$$ \begin{align*} S_{MPSK}(t) =& \sum\limits_{n}^{}g(t - nT_s)A\cos(\omega_c t + \phi_n)\\ =& \left [\sum\limits_{n}^{}A\cos \phi_n g(t - nT_s) \right]\cos \omega_c t + \left [\sum\limits_{n}^{}A\sin \phi_n g(t - nT_s) \right]( - \sin \omega_c t) \end{align*} $$- 所有符号的模相同
- 幅角在 $[0, 2\pi]$ 均匀分布
可以用星座图表示:
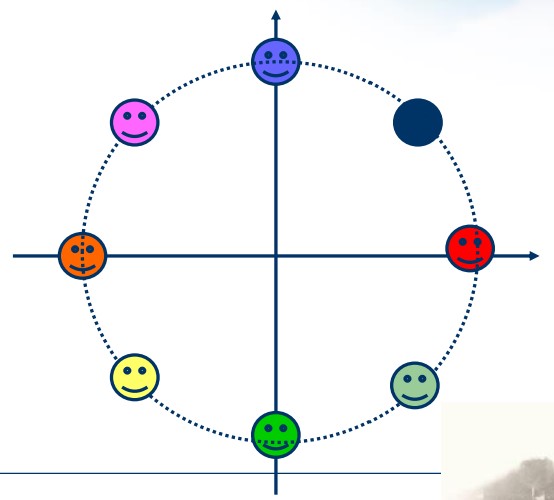
根据信号的 $I, Q$ 表示
计算 MPSK 的 SER:
考虑星座点 $(A, 0)$
接收信号的分布函数为
$$ f(a, b) - \frac{1}{2\pi \sigma_n^2}\exp \left ( -\frac{(a - A)^2 + b^2}{2\sigma_n^2} \right) $$变换到极坐标系
$$ f(\rho, \theta) = \frac{\rho}{2\pi\sigma_n^2}\exp \left ( -\frac{\rho^2 + A^2 - 2A\rho\cos\theta}{2\sigma_n^2} \right)\\ f(\theta) = \int_{0}^{\infty}f(\rho, \theta)\mathrm d\rho = \frac{1}{2\pi}\exp \left ( -\frac{A^2}{2\sigma_n^2}\sin^2\theta \right)\int_{0}^{\infty}\rho\exp \left (-\frac{(\rho - A/\sigma_n\cos\theta)^2}{2} \right)\mathrm d\rho $$误符号率可以表示为
$$ P_{s, MPSK} = 1 - \int_{-\pi/M}^{\pi/M}f(\theta)\mathrm d\theta $$用信噪比表示:
$$ f(\theta) = \int_{0}^{\infty}f(\rho, \theta)\mathrm d\rho = \frac{1}{2\pi}\exp \left ( -\frac{S}{2N}\sin^2\theta \right)\int_{0}^{\infty}\rho\exp \left (-\frac{(\rho - \sqrt{S/N}\cos\theta)^2}{2} \right)\mathrm d\rho $$如果 $S/N$ 很大:
$$ \begin{align*} \int_{0}^{\infty}\rho\exp \left (-\frac{(\rho - \sqrt{S/N}\cos\theta)^2}{2} \right)\mathrm d\rho \approx& \int_{-\infty}^{\infty}\rho\exp \left (-\frac{(\rho - \sqrt{S/N}\cos\theta)^2}{2} \right)\mathrm d\rho\\ =& \sqrt{\frac{S}{N}}\cos\theta \end{align*} $$利用高信噪比近似:
$$ f(\theta) = \sqrt{\frac{S}{2\pi N}}\cos\theta \exp \left ( -\frac{S}{2N}\sin^2\theta \right) $$当 M 比较大时:
$$ \begin{align*} P_{s, MPSK} =& 1 - \int_{-\pi/M}^{\pi/M}\sqrt{\frac{S}{2\pi N}}\cos\theta \exp \left ( -\frac{S}{2N}\sin^2\theta \right)\mathrm d\theta\\ \approx& \frac{2}{\sqrt{\pi}}\int_{\pi/M}^{\infty}\sqrt{\frac{S}{2N}}\cos\theta\exp \left ( -\frac{S}{2N}\sin^2\theta \right)\mathrm d\theta\\ =& \frac{2}{\sqrt{2\pi}}\int_{\pi/M}^{\infty}\exp \left ( -\frac{S}{2N}\sin^2\theta \right)\mathrm d\sqrt{\frac{S}{N}}\sin\theta\\ =& \frac{2}{\sqrt{2\pi}} \int_{\sqrt{S/N}\sin\pi/M}^{\infty}\exp \left ( -\frac{u^2}{2} \right)\mathrm du\\ =& 2Q \left ( \sqrt{\frac{S}{N}}\sin\frac{\pi}{M} \right) \end{align*} $$换算成 BER, $E_b/n_0$
$$ P_{b, MPSK} = \frac{2}{\log_2M}Q \left ( \sqrt{2\log_2M\frac{E_b}{n_0}}\sin\frac{\pi}{M} \right) $$一个简单的方法:
看起来像是先射箭后画靶。

例子2:正交幅度调制 QAM
信号表示
$$ \begin{align*} S_{MQAM}(t) =& \left [\sum\limits_{n}^{}a_n g(t - nT_s) \right]\cos \omega_c t + \left [\sum\limits_{n}^{}b_n g(t - nT_s) \right]( - \sin \omega_c t) \end{align*} $$I,Q 两路的电平集合:
$$ a_n\in \lbrace \pm A, \dots, \pm(M - 1)A \rbrace\\ b_n\in \lbrace \pm A, \dots, \pm(M - 1)A \rbrace\\ $$QAM是一种典型的星座图,它分布于复平面的格点上,其符号的实虚部均为奇数(便于分析)
解调过程:
I 路信息提取:乘以同相载波 $\cos\omega_c t$ ,再低通滤波
Q 路信息提取:乘以同相载波 $-\sin\omega_c t$ ,再低通滤波
差错分析:
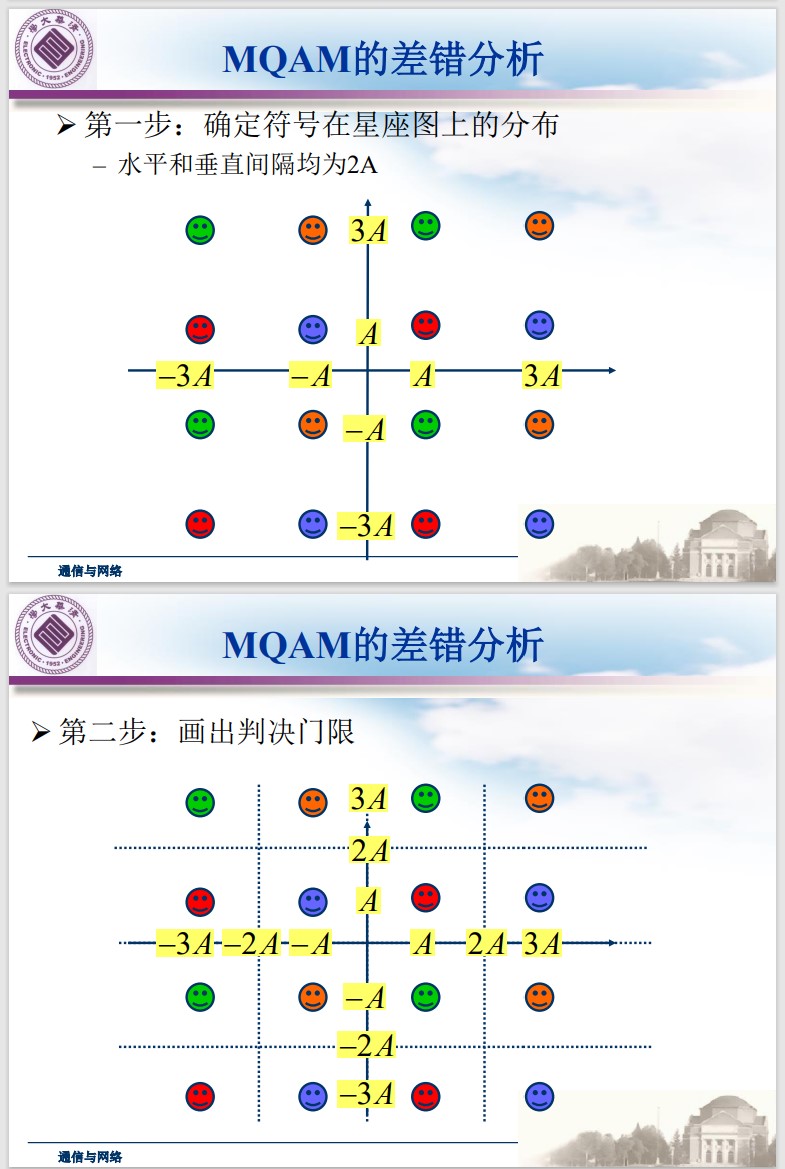
(通过后面的分析可以发现,降低误码率的关键是将符号间的最小距离最大化)
计算各符号的差错概率:
四个角:
$$ P_s = 1 - \left [ 1 - Q \left ( \frac{A}{\sigma} \right) \right]^2 $$ $4(L - 2)$ 个边点: $$ P_s = 1 - \left [ 1 - Q \left ( \frac{A}{\sigma} \right) \right]\left [ 1 - 2Q \left ( \frac{A}{\sigma} \right) \right] $$ $(L - 2)^2$ 个内点: $$ P_s = 1 - \left [ 1 - 2Q \left ( \frac{A}{\sigma} \right) \right]^2 $$计算平均 SEP:
$$ \begin{align*} P_s =& \frac{1}{L^2}\lbrace 4(2Q - Q^2) + 4(L - 2)(3Q - 2Q^2) + (L - 2)^2(4Q - 4Q^2) \rbrace\\ \approx& \frac{4L^2 - 4L}{L^2}Q \left ( \frac{A}{\sigma_n} \right) \end{align*} $$省略了 $Q$ 的高阶量。
计算平均功率:
$$ S = 2 \times \frac{2A^2}{L}[1^2 + 3^2 + \dots + (L - 1)^2] = \frac{2(L^2 - 1)}{3}A^2 $$是同A的LPAM功率的两倍。因为MQAM有两路LPAM
得到 SEP:
$$ P_s = \frac{4M - 4L}{M} Q \left (\sqrt{\frac{3}{2(M - 1)}\frac{S}{N}} \right)\\ M = L^2 $$得到 BEP:
$$ P_b = 4 \left (1 - \frac{1}{\sqrt M} \right) Q \left (\sqrt{\frac{3\log_2M}{2(M - 1)}\frac{E_b}{n_0}} \right) \approx 4Q\left (\sqrt{\frac{3\log_2M}{2(M - 1)}\frac{E_b}{n_0}} \right)\\ $$注意到MQAM可以看成两路正交的MPAM
$$ \begin{align*} P_{s, MQAM} =& 1 - (1 - P_{LPAM})^2\\ \approx& 2P_{LPAM}\\ =& 4 \left ( 1 - \frac{1}{\sqrt M} \right)Q \left ( \sqrt{\frac{3}{(M - 1)}\frac{S/2}{N}} \right) \end{align*} $$这个推导方式更简单。
QAM 是在独立解映射条件下最好的方案。但是距离高斯信道容量还有一定距离。要达到更好的信道容量,可以采用联合解映射,将译码过程联合起来。
例子3:频移键控 FSK
一般来说,信号表达式和调制框图的相互反演是比较容易做的
相对于PAM,PSK和QAM,FSK占用更大的频带,
相干解调
Coherent Demodulation
反思FSK非相干解调方式,如果对每个频率的载波进行匹配,则可以提高信噪比
这种方法需要本地子载波
解调器的结构和非相干解调很像
无法用星座图方法表示,但是可以用类似的信号空间表示
若MFSK载频等间隔,则调制阶数约高,占用带宽越大
如果每次可以选择多个载频,甚至控制载频幅度,则可承载的符号量可以获得极大提升。由此便引申出OFDM技术
- 通过调制FSK的每个载波的幅度相位,可以承载更多的信息
星座图没法表述 FSK. 可以使用信号空间方法来表示。
差错分析:
FSK 的判决门限为棱锥形状:
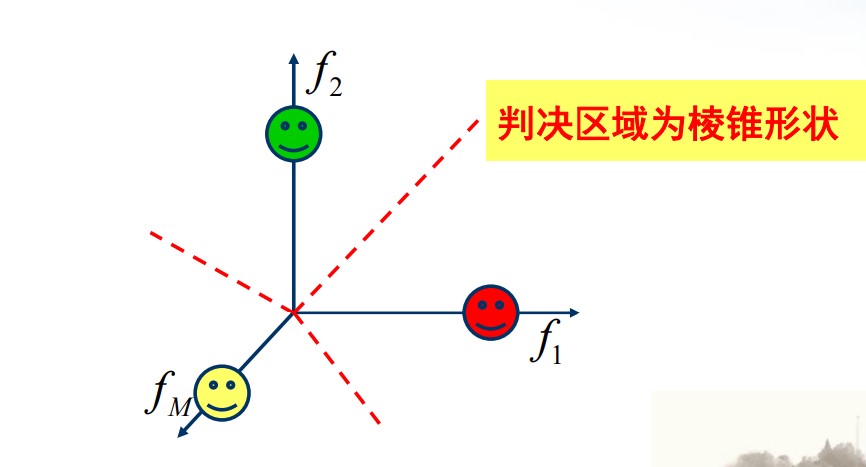
根据对称性,可以只考虑一个符号的差错概率。
考虑 FSK 信号
$$ [A, 0, \dots, 0] $$匹配滤波的输出为
$$ [A + n_1, n_2, \dots, n_M] $$正确判决:信号落在本棱锥中
$$ A + n_1 \gt n_i, i = 2, \dots, M $$被判决符号的条件分布为
$$ f_{[A + n_1, n_2, \dots, n_M]}(\vec r) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp \left ( -\frac{(r_1 - A)^2}{2\sigma^2} \right)\prod_{i = 2}^M\frac{1}{\sqrt{2\pi \sigma^2}}\exp \left ( -\frac{r_i^2}{2\sigma^2} \right) $$不满足正确判决条件的概率为
$$ \begin{align*} P_s =& 1 - \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi \sigma^2}}\exp \left ( -\frac{(r_1 - A)^2}{2\sigma^2} \right)\prod_{i = 2}^M \int_{-\infty}^{r_1}\frac{1}{\sqrt{2\pi \sigma^2}}\exp \left ( -\frac{r_i^2}{2\sigma^2} \right)\mathrm dr_i\mathrm dr_1\\ =&1 - \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi \sigma^2}}\exp \left ( -\frac{(r_1 - A)^2}{2\sigma^2} \right)\left (\int_{-\infty}^{r_1}\frac{1}{\sqrt{2\pi \sigma^2}}\exp \left ( -\frac{r_i^2}{2\sigma^2} \right)\mathrm dr_i \right)^{M - 1}\mathrm dr_1 \end{align*} $$记 $x = \frac{r_1}{\sigma}$
$$ \begin{align*} P_s =& 1 - \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi }}\exp \left ( -\frac{(x - A/\sigma)^2}{2} \right)\left (1 - Q(x)\right)^{M - 1}\mathrm dx\\ =& 1 - \frac{1}{\sqrt{2\pi }}\int_{-\infty}^{\infty}\exp \left ( -\frac{u^2}{2} \right)\left (1 - Q \left (u + \frac{A}{\sigma} \right)\right)^{M - 1}\mathrm du \end{align*} $$ $$ \frac{A}{\sigma} = \sqrt{\frac{S}{N}} = \sqrt{\log_2M\frac{2E_b}{n_0}} $$可得 SEP 的表达式
$$ \begin{align*} P_s =& 1 - \frac{1}{\sqrt{2\pi }}\int_{-\infty}^{\infty}\exp \left ( -\frac{u^2}{2} \right)\left (1 - Q \left (u + \sqrt{\frac{S}{N}} \right)\right)^{M - 1}\mathrm du\\ =& 1 - \frac{1}{\sqrt{2\pi }}\int_{-\infty}^{\infty}\exp \left ( -\frac{u^2}{2} \right)\left (1 - Q \left (u + \sqrt{\log_2M\frac{2E_b}{n_0}} \right)\right)^{M - 1}\mathrm du \end{align*} $$另一种简单估界:

正交 2FSK 信号在最佳接收条件时的错误概率为
$$ P_{b,NCFSK} = Q(\sqrt{E_b/n_0}) $$随着 M 的增加,MFSK 的差错性能渐优,这是以带宽的占用为代价的。
PAM, QAM, ASK 等技术随着符号个数的增加,差错性能是越来越差。
FDM——Frequency Division Multiplexing
- 先将各路信号调制到不同频段,然后复用整个
通信带宽 - 信道的非线性会在FDM系统中产生交调失真与
高次谐波,引起路际串话,因此,对信道的非
线性失真要求很高。此外,FDM用到的模拟滤
波器设计较为复杂。
OFDM 基本原理
Orthogonal Frequency division multiplexing
- 把一串高速数据流分解为若干速率低得多的子数据流。
- 将每个子数据流放置在对应的子载波上。
- 将多个子载波合成,一起并行传输。
- 优点:频谱利用率高。
正交性的定义:
$$ \int_{0}^{T}S_1(t)S_2(t)\mathrm dt = 0 $$设相邻子载波的频率间隔为 $1 / T$ , $T$ 为 OFDM 符号的持续时间,则
任意一对子载波的内积满足
带宽 $W$ 和 $B$ 的区别:
物理带宽 $W$
信号带宽 $B$ :半功率带宽(3dB),等效噪声带宽,谱零点带宽,功率比例带宽,最低功率谱带宽
带通信号的表示方法
$$ x(t) = A(t) \cos [\omega_c t + \varphi (t)]\\ $$同相分量: $x_I(t) = A(t) \cos(\varphi(t))$
正交分量: $x_Q(t) = A(t) \sin(\varphi(t))$
与幅度相位的关系:
$$ A(t) = \sqrt{x_I^2(t) + x_Q^2(t)}\\ \varphi(t) = \tan^{-1} \left [ \frac{x_Q(t)}{x_I(t)} \right] $$带通信号的基带表示的方法
$$ x_{bb}(t) = x_I(t) + jx_Q(t)\\ $$解析信号表示
$$ x_A(t) = x_{bb}(t)e^{j\omega_ct}\\ x(t) = \real \lbrace {x_A(t)} \rbrace = \real \lbrace x_{bb}(t)e^{j\omega_ct} \rbrace $$原始带通信号是解析信号的实部
从带通信号恢复基带信号?
$$ \breve{x}(t) = x(t) \circledast h(t)\\ h(t) = \frac{1}{\pi t}\\ \breve{x}(t) = \frac{1}{\pi} \int_{-\infty}^{\infty}\frac{s(\tau)}{t - \tau}\mathrm d\tau\\ H(f) = -j \cdot \text{sgn}(f) = \begin{cases} -j, &f\gt 0\\ 0, &f=0\\ j, &f < 0 \end{cases} $$构造解析信号
$$ x_A(t) = x(t) + j\breve{x}(t)\\ $$频谱分析
$$ X_A(\omega) = [1 + \text{sgn}(\omega)]X(\omega) = \begin{cases} 2X(\omega), &\omega \gt 0\\ X(0) = 0, &\omega = 0\\ 0, &\omega \lt 0 \end{cases}\\ X_{bb} = X_A(\omega + \omega_c) $$带通信道
具有实数值的信道冲激响应(CIR) $h(t)$
等效的解析冲激响应 $h_A(t) = h(t) + j\breve{h}(t)$
任意载波频率 $\omega_c$ 的等效基带冲激响应CIR
$$ h_{bb}(t) = h_A(t) \cdot e^{-j\omega_c t} $$带通收发信号关系 $y(t) = x(t) * h(t)$ ,则
$$ Y(\omega) = H(\omega) X(\omega)\\ Y_A(\omega) = H_A(\omega)X_A(\omega)\\ Y_A(\omega) = [H(\omega) \cdot \frac{1}{2}\left (1 + \text{sgn}(\omega) \right)]X_A(\omega) = \left [ \frac{1}{2}H_A(\omega) \right]X_A(\omega) $$ $H_A(\omega)$ 只有正半轴部分 $$ Y_{bb}(\omega) = Y_A(\omega + \omega_c) = \left [ \frac{1}{2}H_A(\omega + \omega_c) \right]X_A(\omega + \omega_c) = H(\omega + \omega_c) X_{bb}(\omega) $$基带等效系统
$$ y_{bb}(t) = \frac{1}{2}h_{bb}(t) * x_{bb}(t)\\ Y_{bb}(\omega) = H(\omega + \omega_c) X_{bb}(\omega) $$基带时域转移函数 $\frac{1}{2}h_{bb}(t)$
基带频域转移函数 $H(\omega + \omega_c)$
用正交基观点构造了信号波形
$$ x(t) = \sqrt{2}\cos 2\pi f_c t \sum\limits_{k=-\infty}^{\infty}x^I_kg(t - kT_s) + \sqrt{2}\sin 2\pi f_c t \sum\limits_{k=-\infty}^{\infty}x^Q_kg(t - kT_s) $$投影后的噪声:
$$ E \lbrace n_k^In_l^Q \rbrace = 0\\ E \lbrace n_k^In_l^I \rbrace = \delta_{kl}\\ E \lbrace n_k^Qn_l^Q \rbrace = \delta_{kl} $$等效符号差错模型
$$ y_k = x_k + n_k\\ n_k \sim \mathcal{CN}(0, n_0) $$差错控制
差错控制的分类:
- 检错重发 (ARQ)
- 前向纠错 (FEC)
前向纠错的分类:
- 线性码,非线性码
- 分组码(重点),卷积码
- 系统码,非系统码
编码增益
给定误比特率的情况下,采用纠错编码后, $E_b/n_0$ 的减小量称为编码增益。
简单例子:
重复编码
BSC 重传三次:
$$ 3p_e^2(1 - p_e) + p_e^3 \approx 3p_e^2 $$信道编码:通过合理得增加冗余信息,纠正信道传输中可能出现的错误
- 又称为纠错码(Error Correction Coding)
理想信道编码的局限性:
- 码长无穷大
- 没发现代数结构,复杂度太大
如何实用化:
- 有限长。代价:误码率非零,效率低
- 有代数结构。优点:便于译码
评价标准
- 误比特率:评价可靠性
- 码率:评价有效性
分组码
奇偶监督码
- 检错,而非纠错
- 电路实现简单
漏检概率:
$$ P_m =\sum\limits_{i=1}^{\lfloor\frac{n}{2}\rfloor}\binom{n}{2i}\varepsilon^{2i}(1 - \varepsilon)^{n - 2i} $$群计数码
- 累计信息码元中1的个数,以二进制形式放在信息码元后面
- 检错能力
- 强于奇偶校验码
- 当{1变0数量=0变1数}时,无法检出
纠错码的直观表示
- 码字
- 对应 $n$ 维空间的点
Hamming 距离:两个码字之间不同码元的个数
Hamming 距离
- $x_m$ 和 $x_m^\prime$ 中不同取值的位置数 $d_H(\mathbf x_m, \mathbf x_m^\prime)$
- 即模2和中1的个数
汉明码重
- 二进制向量 $\mathbf x_m$ 1的个数 $w(\mathbf x_m)$
最小距离
一个分组码中任意两个码字的最小汉明距离 $d_{\text{min}}$
(n,k)纠错码
$$ B = E + A, \forall A \in \chi\\ S = BH^T = EH^T\\ $$ $S$ 与 $A$ 无关, $A$ 只是无用的陪同(coset)。陪集首:上述陪集的特征由 $S = EH^T$ 标识,我们称 $E$ 为陪集首。
陪集首一般选择集合中 “1” 最少的元素,这是为了优先标识错误数量较小的差错,这一类差错发生的概率较大。
码重:
$$ w(A) =\sum\limits_{i=1}^{n}\mathbf 1 \lbrace a_i = 1 \rbrace = d_H(A, 0) $$001 -> 0,0,0,0,0,1 -> 101
010 -> 0,0,0,0,1,0 -> 011
011 -> 0,0,0,1,0,0 -> 110
100 -> 0,0,1,0,0,0 -> 001
101 -> 0,1,0,0,0,0 -> 010
110 -> 1,0,0,0,0,0 -> 100
111 -> 0,1,0,0,0,1 -> 111
交织器
线性码的改进:
- 上述线性码,均适合于纠正零散错误
- Hamming码对于2个以上的差错就无能为力
- 若差错总是成对出现,则Hamming码基本没用
- 在通信系统中,往往存在不可抗拒的突发错误
例如:无线信道的衰落引起的误码
抗突发误码的方法:交织器
基本原理
- 为了对付突发的信道差错,交织器改变发送码元的时
间顺序 - 将原本相邻的码元在时间上的距离最大化
- 例子:考虑一个(n, k)分组码,其交织后的输出为
将突发误码转换成零星误码
交织器的性能:
宽度
- 就是分组码的码长n
- 决定于所采用的分组码
深度
- 深度m决定了相邻码元交织后的间隔
- m又称交织深度
- 若分组码能纠b个突发错误,则交织后能纠mb个突发错误
解交织:
- 从另一个角度来看,解交织打散了突发误码
- 化整为零后的零散误码,就可以交给解码器对付了
卷积码
输入无限长的激励,则输出信号无限长,
若冲激响应有限,则输出只与某一段输入有关
卷积码的参数 $n, k, N$
约束长度,信息码位,每次输出
使用树状图进行分类讨论
树状图的冗余:
- 树状图具有很多冗余表示
树状图的应用:计算最小码距
- 分组码的最小码距定义为非零码字的最小码重
- 和分组码不同,卷积码没有分组的概念
- 约束长度隐含了某种独立性,可以只考虑 $kN$ 的信息比特编码后的非零码字,也就是考虑 $nN$ 个非零的编码输出位
状态图的应用
- 自由距:无限长信息序列编码后的最小汉明距离
- 自由距不等于最小距
自由距等于寄存器从零状态开始,经过非零状态,然后回到零状态的输出1的个数的最小值
卷积码的译码
维特比译码
网格图
最大似然下的最优译码
- 低复杂度
- 采用最小汉明距离作为代价函数
采用动态规划的卷积码译码成为 viterbi 译码
- viterbi 译码的起始状态是 0 状态
- viterbi 译码没有确定的代价函数,
分组码译码可以知道是否译码错误了。通过校验矩阵来校验就行了。
但是 viterbi 译码并不能肯定译码结果是否正确。
硬判决和软判决
硬判决:任务是检测和矫正误码
软判决:应用于卷积/ Viterbi 译码器,迭代译码
检错重发 ARQ
$P_c = (1 - \varepsilon)^n$ 为正确概率 $P_d$ 检出错误概率 $P_m$ 漏检概率 $$ P_c + P_d + P_m = 1 $$总分组差错概率
$$ P_b = P_m + P_dP_m + P_d^2P_m + \dots = \frac{P_m}{1 - P_d} = \frac{P_m}{P_c + P_m} $$停等ARQ
收到上一个 ACK/NAK 再发送下一个包或者重传上一个包
假设发送方一直传输(一次就能传输成功),吞吐量的上限为
$$ \eta_{sw, 0} = \frac{k}{T_DR}\\ T_D = T_m + 2 T_d + T_c + T_a = T_m + T_{dca} = \frac{k}{n + T_{dca}R} $$若有完美的差错检出能力 $P_d = 1 - (1 - \varepsilon)^n$
则
$$ \eta_{sw} = \frac{k/n}{1 + T_{dca}R/n}(1 - \varepsilon)^n $$返回 N-ARQ
不等 ACK/NAK 返回就传下一个包,若检错则重传从错误开始的所有包
$$ \eta_{GBN, 0} = \frac{k}{n} $$