Statistical Signal Processing

参数估计

分类：

• 经典估计
• 贝叶斯估计

准则：

• MSE，均方误差

$$ \hat \theta = f(\bm{x}) $$

MSE

$$ \text{mse}(\hat \theta) = E \lbrace(\theta - \hat \theta)^2\rbrace = \text{var}(\hat \theta) + b^2(\hat \theta)\\ b^2(\hat \theta) = E(\hat \theta) - \theta $$

现实中无法直接计算 MSE，因为涉及到真值 $\theta$，但是 $\theta$ 是我们要求的参数。

MVU

最小方差无偏估计

MVU, Minimum Variance Unbiased

无偏：

$$ E(\hat \theta) = \theta, a \lt \theta \lt b $$

无偏的含义：$\hat \theta$ 的求法需要对取值范围内任意的 $\theta$ 进行估计。

无偏估计是否一定存在？不一定。

最小方差：

$$ \min \text{var}\lbrace\hat\theta\rbrace $$

MVU的内涵：估计值的发散程度最小（最小方差），平均意义上靠近真值（MVU）。是对 MSE 的迂回实现。

克拉美罗界定理(CRLB)

假设 $p(\bm{x};\theta)$ 满足正则条件：

$$ E \left [ \frac{\partial\ln p(\bm{x};\theta)}{\partial\theta} \right] = 0 $$

则

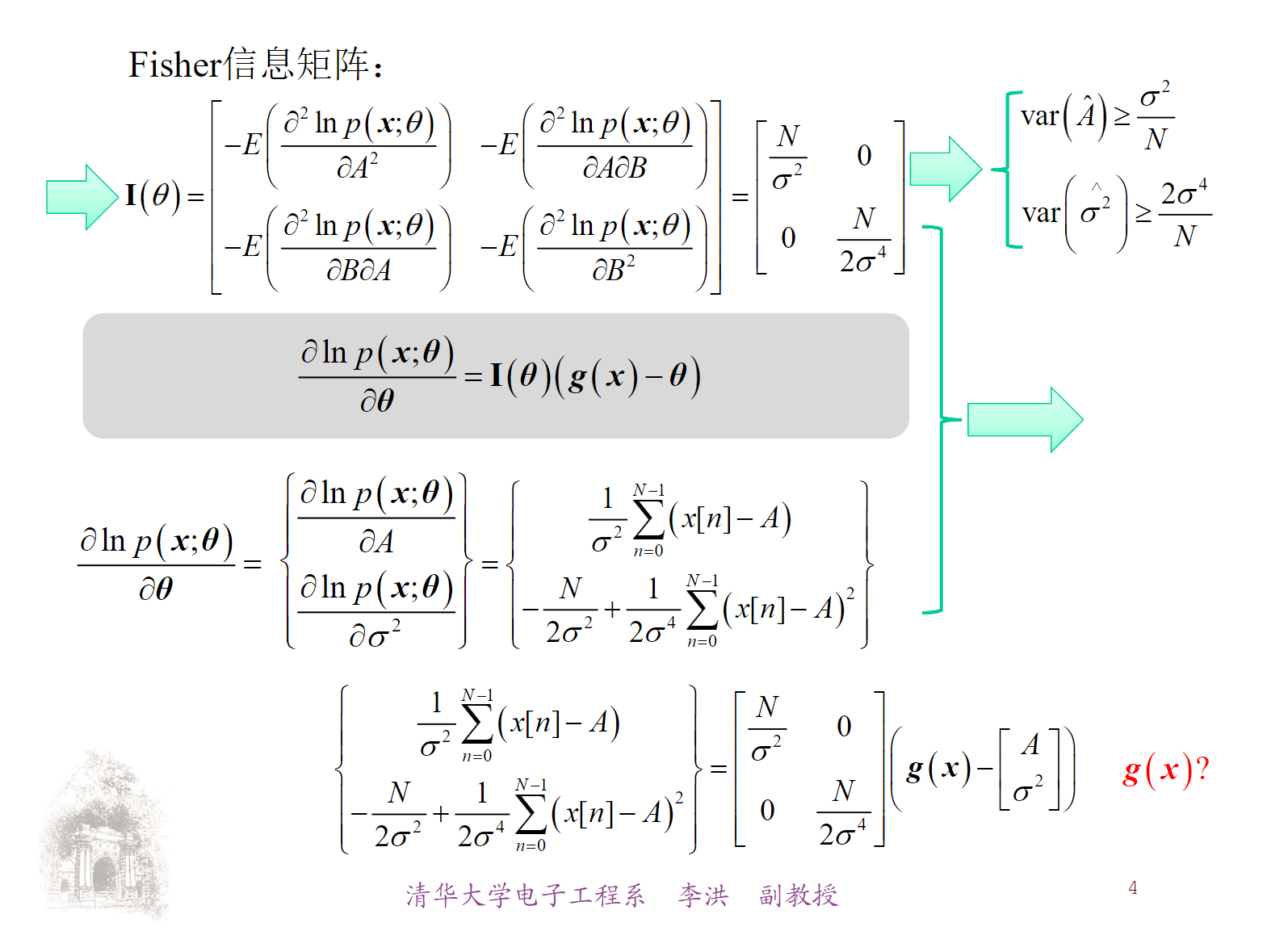
$$ \text{var}(\hat\theta) \ge \frac{1}{E \left [\left( \frac{\partial\ln p(\bm{x};\theta)}{\partial\theta}\right)^2 \right]} = - \frac{1}{E \left [ \frac{\partial^2\ln p(\bm{x};\theta)}{\partial\theta^2} \right]} $$

等号成立的充要条件：找到函数 $I, g$

$$ \frac{\partial \ln p(\bm{x};\theta)}{\partial \theta}= I(\theta)(g(\bm{x}) - \theta)\\ \hat \theta = g(\bm{x}) $$

此时有 $\text{var}(\hat\theta) =1 / I(\theta)$。

求解MVU

$$ \frac{\partial \ln p(\bm{x};A)}{\partial A} = \frac{1}{\sigma^2}\sum\limits_{n=0}^{N - 1}(x[n] - A) = \frac{N}{\sigma^2}\left (\frac{1}{N}\sum\limits_{n=0}^{N - 1}(x[n] - A) \right) $$

$$ g(\bm{x}) = \frac{1}{N}\sum\limits_{n=0}^{N - 1}x[n]\\ I(\theta) = \frac{N}{\sigma^2} $$

有效估计量：能达到克拉美罗下界的估计量，是MVU的子集。

参数变换的克拉美罗界

若

$$ \alpha = g(\theta) $$

则

$$ CRLB(\hat \alpha) = \left(\frac{\partial g(\theta)}{\partial \theta}\right)^2CRLB(\hat \theta) $$

对于高斯分布有

$$ E(x^2) = \mu^2 + \sigma^2\\ E(x^4) = \mu^4 + 6\mu^2\sigma^2 + 3\sigma^4 $$

当数据量很大时

有效估计量靠近真值：$N \rightarrow \infty, \hat\theta \rightarrow \theta$

非线性变换渐进有效,可以看成线性函数：$g(\hat \theta) \approx g(\theta) + \frac{\partial g(\theta)}{\partial\theta}(\hat \theta - \theta)$

矢量参数的克拉美罗界

$$ E \left [ \frac{\partial \ln p(\bm{x};\bm{\theta})}{\partial \bm{\theta}} \right] = 0 $$

$$ \alpha = g(\theta) $$

注意：$\bm T(\bm x)$ 的维度要和 $\bm \theta$ 的维度相同

线性模型方法

$$ x = H\theta + w, w \sim N(0, \sigma^2I) $$

$$ p(x;\theta) = \frac{1}{(2\pi\sigma)^{N/2}}\exp \lbrace -\frac{1}{2\sigma^2}(x - H\theta)^T(x - H\theta) \rbrace $$

$$ \frac{\partial \ln p(x;\theta)}{\partial \theta} = \frac{H^TH}{\sigma^2}\lbrace (H^TH)^{-1}H^Tx - \theta \rbrace $$

从而

$$ \hat \theta = (H^TH)^{-1}H^Tx\\ C_{\hat\theta} = \sigma^2(H^TH)^{-1} $$

这个 MVU 估计量满足

$$ \hat \theta \sim N(\theta, \sigma^2(H^TH)^{-1}) $$

• 要求观测数据与待估计参数间呈线性关系
• 要求噪声是高斯白噪声
• 要求观测矩阵是满秩的
• 所得估计量是有效估计量

一般信号模型

$$ x = H\theta + s + w, s已知，w \sim N(0, C) $$

结论

$$ \hat \theta = (H^TC^{-1}H)^{-1}H^TC^{-1}(x - s)\\ C_{\hat\theta} = (H^TC^{-1}H)^{-1} $$

充分统计量方法

$$ p(x|T(x);\theta) = p(x|T(x)) $$

则称 $T(x)$ 为充分统计量

充分统计量的性质:

• 一旦充分统计量确定，似然函数就与待估计参数无关
• 充分统计量依赖于待估计参数。待估计参数变化，其相应的充分计量一般也会变化
• 所谓“充分”，是相对于原始观测数据而言的原始观测量总是充分统计量，但通常不是最小集
• 充分统计量并不唯一

若

$$ \int_{-\infty}^{\infty}v(T)p(T;\theta)\mathrm dT = 0 $$

对所有的 $\theta$ 并非都满足，只对零函数 $v(T) = 0$ 成立，则称充分统计量是完备的。

• 一般地，当待估计参数发生变化时，充分统计量也会发生变化
• 一旦充分统计量确定以后，似然函数就与待估计参数无关

Neyman-Fisher因子分解定理

如果概率密度函数（或概率质量函数，对于离散随机变量）$p(x; \theta)$ 可以被分解为

$$ p(x; \theta) = g(T(x); \theta) \cdot h(x) $$

其中：

• $g(T(x); \theta)$ 是一个只通过统计量 $T(x)$ 并依赖于参数 $\theta$ 的函数。
• $h(x)$ 是只与观测数据 $x$ 相关的函数，与参数 $\theta$ 无关。

那么，统计量 $T(x)$ 是参数 $\theta$ 的充分统计量。反之，如果 $T(x)$ 是参数 $\theta$ 的充分统计量，那么概率密度函数 $p(x; \theta)$ 必然可以分解为上述形式。

Rao-Black-Lehmann-Scheffe(RBLS)定理

若 $\breve\theta$ 是$\theta$的无偏估计，$T(x)$是$\theta$的充分统计量，那么$\hat \theta=E(\breve{\theta}|T(x))$

1. 是$\theta$ 的一个适用的估计量(与$\theta$无关)
2. 无偏的
3. 对所有的 $\theta$，它的方差小于等于$\breve\theta$ 的方差
4. 若$T(x)$是完备的，那么$\theta$是MVU估计量

矢量参数的 RBLS

BLUE

定义

直接求出数据->参数的映射 $\bm A_{p \times N}$：

$$ \bm x = \bm H \theta\\ \hat {\theta}_{p \times 1} = \bm A\bm x $$

无偏性：

$$ \theta = E(\hat\theta) = \bm AE(\bm x) = \bm AH\theta\\ \Rightarrow AH = I_{p \times p} $$

最佳（最小方差）

$$ \min \lbrace a_i^TCa_i \rbrace, A = [a_1, a_2, \dots, a_n]^T $$

其中

$$ C = E \lbrace (x - E(x))(x - E(x))^T \rbrace $$

高斯-马尔可夫定理

如果数据具有一般线性模型的形式

$$ \bm x = \bm H \theta + w $$

其中 $\bm H$ 为已知 $N \times p$ 矩阵，$\theta$ 为待估计参数，$w$ 是均值为零、协方差为 $\bm C$ 的噪声矢量（不一定为高斯），则 BLUE 估计量为

$$ \hat \theta = (H^TC^{-1}H)^{-1}H^TC^{-1}x\\ C_{\hat\theta} = (H^TC^{-1}H)^{-1} $$

• 若为高斯噪声，则BLUE为MVU，且为有效估计量

MLE

定义

$$ \hat \theta = \arg\max\limits_\theta p(\bm{x};\theta) $$

如果 PDF 可导

$$ \frac{\partial p(\bm x; \theta)}{\partial \theta}\bigg|_{\hat\theta} = 0\\ \Rightarrow\frac{\partial \ln p(\bm x; \theta)}{\partial \theta}\bigg|_{\hat\theta} = 0 $$

若有效估计量存在，$\frac{\partial \ln p(\bm x; \theta)}{\partial \theta}\bigg|_{\hat\theta} = I(\theta)(g(x) - \theta)$，则可以使用最大似然估计方法求得结果。

MLE 的性质

如果数据 $\bm x$ 的 PDF $p(\bm x;\theta)$ 满足“正则”条件，那么
对于足够多的数据记录，未知参数 $\theta$ 的 MLE 渐近服从

$$ \hat\theta \stackrel{a}{\sim} N(\theta, I^{-1}\theta) $$

其中 $\theta$ 是在未知参数真值处计算的 Fisher 信息。

MLE是渐近无偏的

MLE渐近达到CRLB

MLE是渐近有效的

MLE是渐近最佳的

• MLE的方差（协方差）可大于、等于、小于CRLB！（不同于MVU估计）
• 但数据量足够多时，将与CRLB接近
• 因此，可利用CRLB评估MLE的性能

“足够多”数据：大量能带来新信息的数据

MLE的不变性

若参数 $\alpha = g(\theta)$，则

$$ \hat\alpha = g(\hat\theta) $$

若 $g$ 非一对一函数，那么 $\hat\alpha$ 是使修正后的似然函数 $p_T(\bm x;\alpha)$ 最大者

$$ \hat\alpha = \arg\max_\alpha p_T(\bm x; \alpha)\\ p_T(\bm x; \alpha) = \max_{\theta: \alpha=g(\theta)}p(\bm x; \theta) $$

该性质对函数 $g$ 无线性变换要求，对任意函数均成立。

对比MVU

• 无偏性、有效性仅对线性变换成立
• 对非线性变换不能保持（但渐近无偏、渐近有效）

对一般线性模型，MLE是MVU，达到了CRLB，是有效的、最佳的！

最小二乘估计(LS)

线性最小二乘估计

加权最小二乘估计

约束最小二乘估计

比较

经典估计方法比较

噪声电平估计问题

$$ x[n] = A + w[n] $$

其中 $w[n] \sim N(0, \sigma^2)$，待估计参数 $\theta = [A, \sigma^2]^T$

MVU估计

$$ p(x;\theta) = \frac{1}{(2\pi\sigma^2)^{N/2}}\exp \lbrace -\frac{1}{2\sigma^2} \sum\limits_{n=0}^{N - 1}(x[n] - A)^2\rbrace $$

$$ \frac{\partial \ln p (x;\theta)}{\partial A} = \frac{1}{\sigma^2}\sum\limits_{n=0}^{N - 1}(x[n] - A) $$

$$ \frac{\partial \ln p(x;\theta)}{\partial \sigma^2} = \frac{N}{2\sigma^2} + \frac{1}{2\sigma^4}\sum\limits_{n=0}^{N - 1}(x[n] - A) $$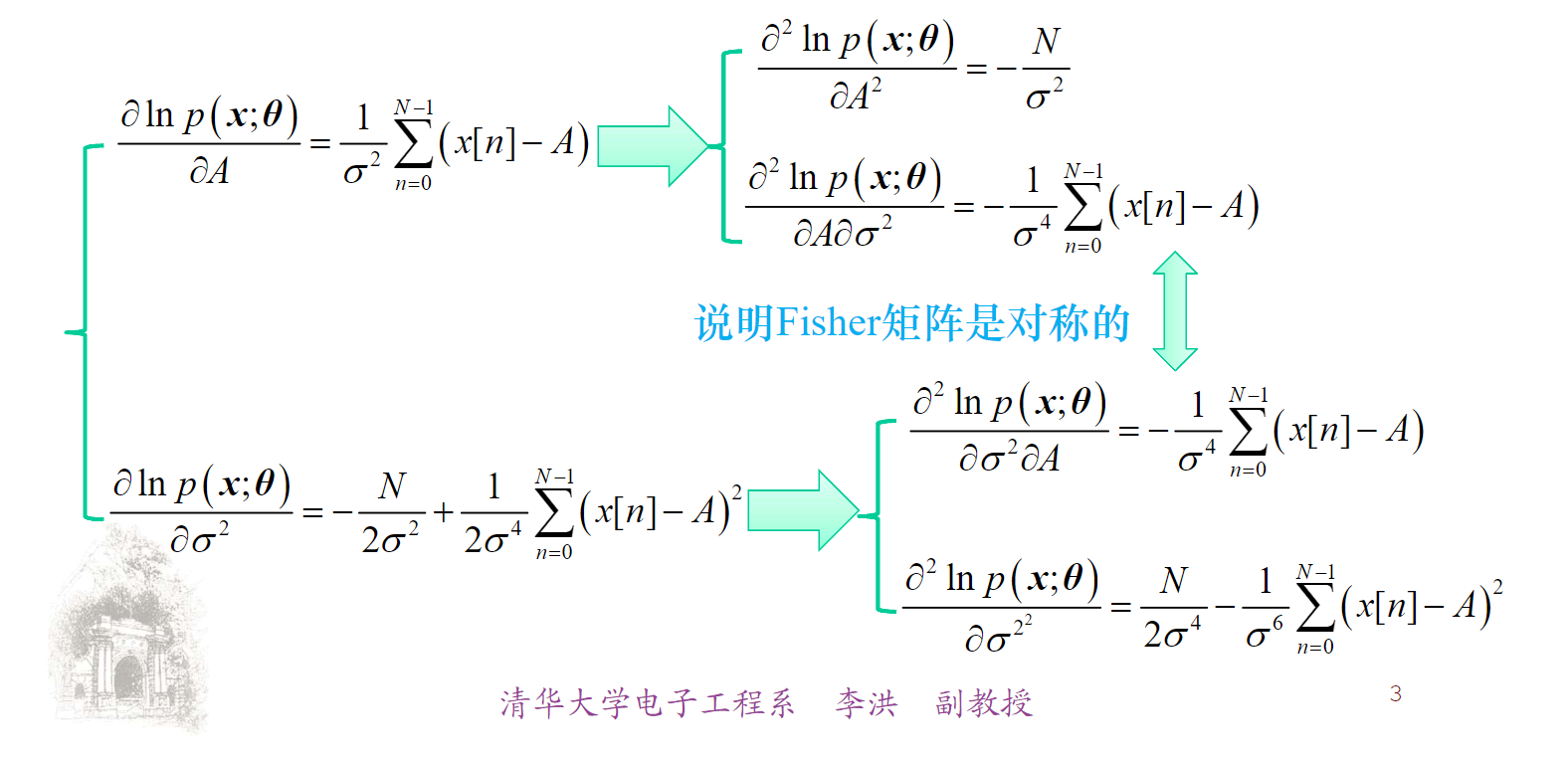

线性模型

$$ \hat\theta = (\bm H^T\bm H)^{-1}\bm H^T x $$

BLUE

$$ \hat\theta = (\bm H^T\bm C^{-1}\bm H)^{-1}\bm H^T\bm C^{-1} x $$

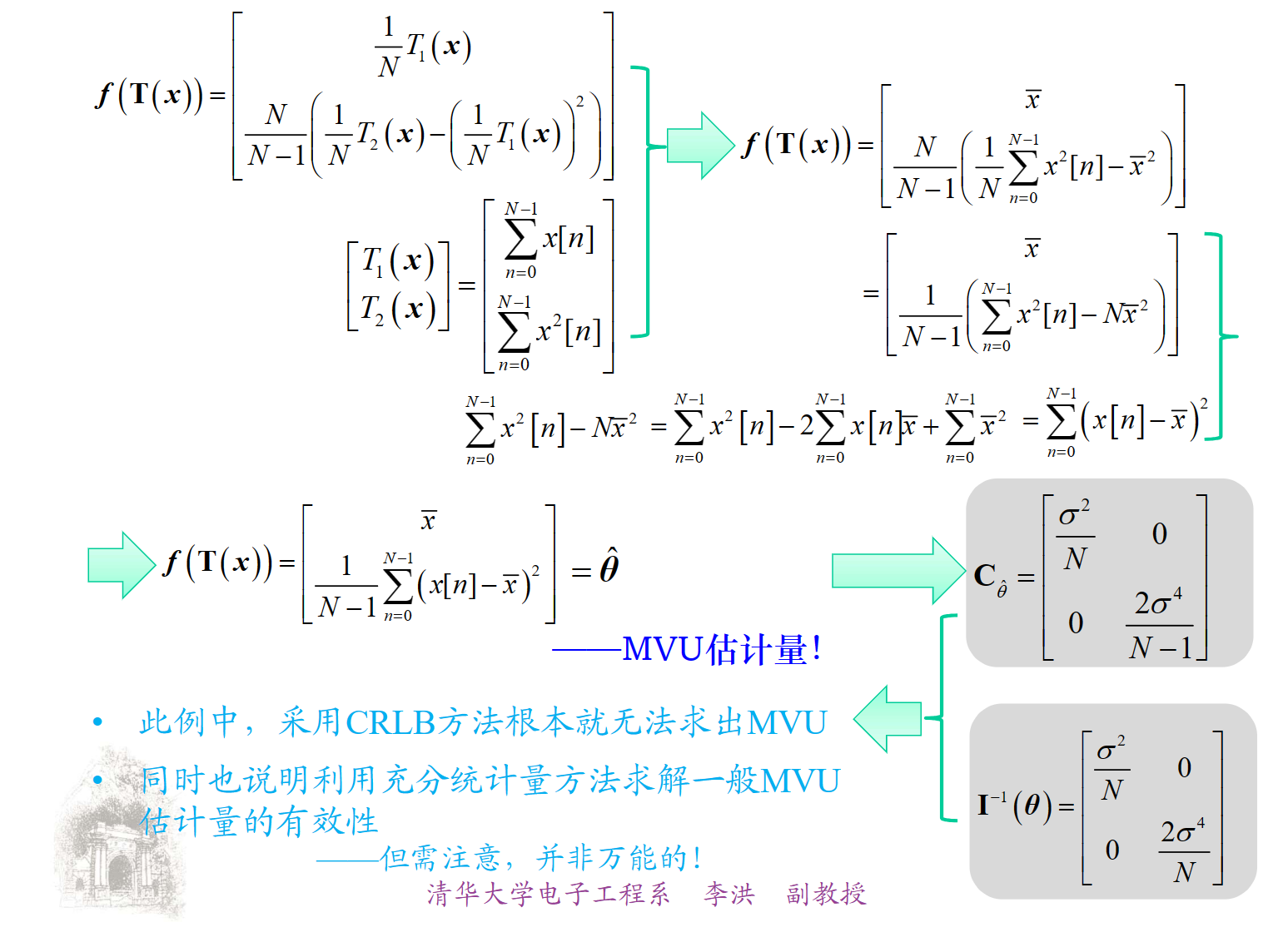
充分统计量

MLE

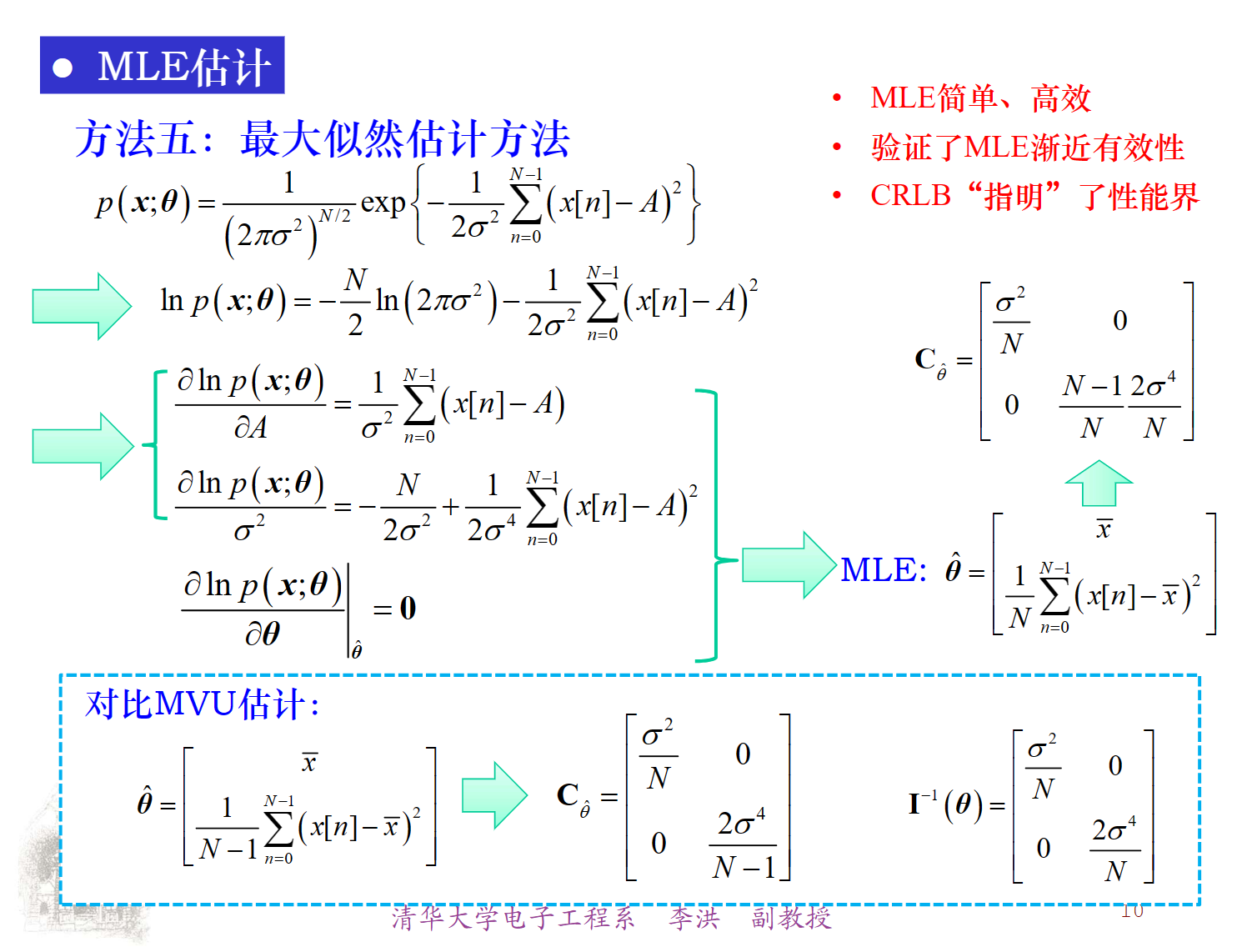
LSE

贝叶斯估计

贝叶斯MSE：
Bmse$\left(\hat{\theta}\right)=E\left(\left(\theta-\hat{\theta}\right)^2\right)$

$=\int\int\left(\theta-\hat{\theta}\right)^{2}p\big(\mathbf{x},\theta\big)d\mathbf{x}d\theta$ $=\iint\left(\theta-\hat{\theta}\right)^2p\big(\boldsymbol{x}|\theta\big)p\big(\theta\big)d\boldsymbol{x}d\theta$
$=\iint\left(\theta-\hat{\theta}\right)^2p(x|\theta)dxp(\theta)d\theta$

$\hat{\theta}=E\big(\theta|x\big)$

多余参数：未知，但不感兴趣的参数
解决思路：通过积分消除多余参数的影响
(1) 后验概率中存多余参数时：

$$ p(\boldsymbol{\theta},\boldsymbol{\alpha}\mid\boldsymbol{x}) \Rightarrow p (\boldsymbol{\theta}\mid\boldsymbol{x})=\int p(\boldsymbol{\theta},\boldsymbol{\alpha}\mid\boldsymbol{x})\:d\boldsymbol{\alpha} $$

(2) 条件概率中存在多余参数时：

$$ p(\boldsymbol{\theta}\mid\boldsymbol{x})=\frac{p(\boldsymbol{x}\mid\boldsymbol{\theta})p(\boldsymbol{\theta})}{\int p(\boldsymbol{x}\mid\boldsymbol{\theta})p(\boldsymbol{\theta})d\boldsymbol{\theta}} $$

$$ \text{若现只有 }p(x|\theta,\alpha)\text{,而无 }p(x|\theta) $$

此时可通过积分方式解决

$$ p(x\mid\theta)=\int p(x\mid\theta,\alpha)p(\alpha\mid\theta)d\alpha $$

进一步地，若待估计参数与多余参数相互独立，

$$ p(x\mid\theta)=\int p(x\mid\theta,\alpha)p(\alpha)d\alpha $$

矢量参数下贝叶斯估计
若 θ 是 $p{\times}1$ 的矢量参数，那么为了估计其中某个参数 $\theta_i$, 可以将剩余参数当作多余参数，因此对$\theta_i$ 的MMSE为

$$ \hat{\theta}_i=E\left(\theta_i\mid x\right)=\int\theta_ip(\theta_i\mid x)d\theta_i $$

其中

$$ p(\theta_i\mid x)=\int\cdots\int p(\theta\mid x)d\theta_1\cdots d\theta_{i-1}d\theta_{i+1}\cdots d\theta_p $$

$$ \hat{\theta}_i=\int\theta_i\left(\int\cdots\int p(\boldsymbol{\theta}\mid\boldsymbol{x})\underline{d\theta_1\cdots d\theta_{i-1}d\theta_{i+1}\cdots d\theta_p}\right)d\theta_i=\int\theta_ip(\boldsymbol{\theta}\mid\boldsymbol{x})d\boldsymbol{\theta} $$

$$ \Longrightarrow\hat{\theta}=\begin{bmatrix}\theta_1p(\theta|x)d\theta\\\int\theta_2p(\theta|x)d\theta\\\vdots\\\int\theta_pp(\theta|x)d\theta\end{bmatrix}=\int\theta_P(\theta|x)d\theta=E(\theta|x) $$

Woodbury 恒等式：

$$ \left(\mathbf{B}+\boldsymbol{u}\boldsymbol{u}^T\right)^{-1}=\mathbf{B}^{-1}-\frac{\mathbf{B}^{-1}\boldsymbol{u}\boldsymbol{u}^T\mathbf{B}^{-1}}{1+\boldsymbol{u}^T\mathbf{B}^{-1}\boldsymbol{u}} $$

贝叶斯风险

$$ \Re=\iint C(\varepsilon)p(x,\theta)dxd\theta $$

二次型误差

$$ C(\varepsilon) = \begin{pmatrix}\theta-\hat{\theta}\end{pmatrix}^2 $$

这就是 MMSE

此时为平均值。

绝对误差

$$ C(\varepsilon)=\begin{vmatrix}\theta-\hat{\theta}\end{vmatrix} $$

Leibnitz 准则
$\frac{\partial}{\partial u}\int\limits_{\phi_1(u)}^{\phi_2(u)}h\big(u,v\big)dv=\int\limits_{\phi_1(u)}^{\phi_2(u)}\frac{\partial h\big(u,v\big)}{\partial u}dv+\frac{\partial\phi_2\big(u\big)}{\partial u}h\big(u,\phi_2\big(u\big)\big)-\frac{\partial\phi_1\big(u\big)}{\partial u}h\big(u,\phi_1\big(u\big))$

此时

$$ \int_{-\infty}^{\hat{\theta}}p\big(\theta|x\big)d\theta=\int_{\hat{\theta}}^{+\infty}p\big(\theta|x\big)d\theta $$

为中位数

成功失败型误差

$$ C(\varepsilon)=\begin{cases}0,\left|\theta-\hat{\theta}\right|<\delta\\1,\left|\theta-\hat{\theta}\right|\geq\delta\end{cases} $$

此时

$$ \hat{\theta}=\arg\max_{\theta}p(\theta|x) $$

即 $\hat{\theta}$ 是后验PDF的最大值 (众数)

MAP maximum a posteriori

根据贝叶斯公式

$$ \hat{\theta}=\arg\max_{\theta}\left\lbracep(x|\theta)p(\theta)\right\rbrace\\ \hat{\theta}=\arg\max_{\theta}\left\{\ln p\big(x|\theta\big)+\ln p\big(\theta\big)\right\} $$

三值比较

一般而言，“三值”并不相等，因此三种估计量往往不同

特例：高斯时“三值”相等，三种估计方法等价

大数据量时先验信息不起作用，最大后验概率估计（MAP）将转变为（贝叶斯）最大似然估计（MLE）

线性贝叶斯估计

线性贝叶斯估计(LMMSE), 也称线性最小意味着：

$$ \hat{\theta}=\sum_{n=0}^{N-1}a_nx[n]+a_N $$

即限定估计量与观察数据间呈线性关系，然最小化

$$ \mathrm{Bmse}\Big(\hat{\theta}\Big)=E\Big[\Big(\theta-\hat{\theta}\Big)^{2}\Big] $$

即，LMMSE:

$$ \min\left\{E\left[\left(\theta-\hat{\theta}\right)^2\right]\right\}\\s.t.\quad\hat{\theta}=\sum_{n=0}^{N-1}a_nx[n]+a_N $$

解得估计量：

$$ \hat{\theta}=E\left(\theta\right)+\mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\left(x-E\left(x\right)\right)\\\mathrm{Bmse}\left(\hat{\theta}\right)=\mathbf{C}_{\theta\theta}-\mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\mathbf{C}_{x\theta} $$

对比 MMSE：

附加了线性约束

• 可得显示解——好求
• 仅需一阶矩和二阶矩

无附加约束

• 可能难以求得显示解
• 需PDF
• 全局最优
• 仅在“线性”中最优

矢量参数情况

待估计参数$\boldsymbol{\theta}=\begin{bmatrix}\theta_1,\theta_2,…,\theta_p\end{bmatrix}^T$,其每个参数的 LMMSE 定义为

$$ \begin{aligned}&\min E\bigg[\bigg(\theta_{i}-\hat{\theta}_{i}\bigg)^{2}\bigg]\\&s.t.\hat{\theta}_{i}=\sum_{n=0}^{N-1}a_{in}x[n]+a_{iN}\end{aligned} $$

$$ \hat{\boldsymbol{\theta}}=\begin{bmatrix}E(\theta_1)\\E(\theta_2)\\\vdots\\E(\theta_p)\end{bmatrix}+\begin{bmatrix}\mathbf{C}_{\theta_1x}\mathbf{C}_{xx}^{-1}\left(\boldsymbol{x}-E(\boldsymbol{x})\right)\\\mathbf{C}_{\theta_2x}\mathbf{C}_{xx}^{-1}\left(\boldsymbol{x}-E(\boldsymbol{x})\right)\\\vdots\\\mathbf{C}_{\theta_px}\mathbf{C}_{xx}^{-1}\left(\boldsymbol{x}-E(\boldsymbol{x})\right)\end{bmatrix}\\ =E\left(\boldsymbol{\theta}\right)+\mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\left(\boldsymbol{x} - E(\boldsymbol{x})\right) $$

序贯LMMSE

白噪声电平估计

$$ x[n]=A+w[n],n=0,1,...,N $$

$$ A\sim N\big(0,\sigma_{A}^{2}\big)\\ w[n]\sim N\left(0,\sigma^{2}\right) $$

解得

$$ \begin{aligned} &E(\theta)=0 \\ &\mathbf{C}_{\theta x}=E\left(\left(\theta-E\left(\theta\right)\right)\left(x-E\left(x\right)\right)^{T}\right) \\ &=E\left(\left(A-0\right)\left(x-0\right)^{T}\right) \\ &=E\Big(A\big(A\mathbf{1}+\mathbf{w}\big)^{T}\Big) \\ &=\sigma_{A}^{2}\mathbf{1}^{T} \end{aligned}\\ \begin{aligned} \mathbf{C}_{xx}& =E\left(\left(x-E\left(x\right)\right)\left(x-E\left(x\right)\right)^T\right) \\ &=E\left(\left(A\mathbf{1}+\boldsymbol{w}\right)\left(A\mathbf{1}+\boldsymbol{w}\right)^T\right) \\ &=E\left\{A\mathbf{1}\mathbf{1}^TA+A\mathbf{1}\boldsymbol{w}^T+\boldsymbol{w}\mathbf{1}^TA+\boldsymbol{w}\boldsymbol{w}^T\right\} \\ &=\sigma_A^2\mathbf{1}\mathbf{1}^T+\sigma^2\mathbf{I} \end{aligned}\\ \begin{aligned}\mathbf{C}_{\theta\theta}&=\sigma_A^2\\\mathbf{C}_{x\theta}&=\mathbf{C}_{\theta x}^T\\&=\sigma_A^2\mathbf{1}\end{aligned} $$

$$ \begin{aligned}\hat{A}&=\frac{\sigma_{A}^{2}}{\sigma_{A}^{2}+\frac{\sigma^{2}}{N}}\\\mathrm{Bmse}&\left(\hat{A}\right)=\frac{1}{N}\end{aligned} $$

记

$$ \hat{A}[N-1]=\frac{\sigma_A^2}{\sigma_A^2+\frac{\sigma^2}{N}}\frac{1}{N}\sum_{n=0}^{N-1}x[n] $$

则

$$ \hat{A}[N]=\hat{A}[N-1]+\underbrace{\frac{\sigma_A^2}{\left(N+1\right)\sigma_A^2+\sigma^2}}_{K[N]，增益因子}\Big(x[N]-\hat{A}[N-1]\Big) $$

$$ \frac{\frac1{\sigma^2}}{\frac1{\mathrm{Bmse}\left(\hat{A}\left[N-1\right]\right)}+\frac1{\sigma^2}}=\frac{\mathrm{Bmse}\left(\hat{A}\left[N-1\right]\right)}{\mathrm{Bmse}\left(\hat{A}\left[N-1\right]\right)+\sigma^2}\\=\frac{\frac{\sigma_A^2\sigma^2}{N\sigma_A^2+\sigma^2}}{\frac{\sigma_A^2\sigma^2}{N\sigma_A^2+\sigma^2}+\sigma^2}=\frac{\sigma_A^2}{\left(N\sigma_A^2+\sigma^2\right)+\sigma_A^2}=K\begin{bmatrix}N\end{bmatrix} $$

一般方法

序贯计算方法估计量更新：

$$ \hat{A}[N]=\hat{A}[N-1]+K[N]\Big(x[N]-\hat{A}[N-1]\Big) $$

增益因子：

$$ K\left[N\right]=\frac{\mathrm{Bmse}\left(\hat{A}\left[N-1\right]\right)}{\mathrm{Bmse}\left(\hat{A}\left[N-1\right]\right)+\sigma^2} $$

最小贝叶斯MSE更新：

$$ \mathrm{Bmse}\Big(\hat{A}[N]\Big)\boldsymbol{=}\Big(1\boldsymbol{-}K[N]\Big)\mathrm{Bmse}\Big(\hat{A}[N\boldsymbol{-}1]\Big) $$

初始化：

$$ \hat{A}[-1]=E(A)\\ \text{Bmse}\left ( \hat{A} [ - 1] \right ) = \text{var}\left ( A\right ) $$

维纳滤波

滤波

假定观测数据是零均值、宽平稳的，信号也是零均值、宽平稳的，信号与噪声不相关

$$ x[n] = s[n] + w[n], n = 0, 1, \dots, N - 1 $$

$$ \theta=s[n]\text{ 用 }x[0],x[1],x[2],...,x[n]\text{来估计}$$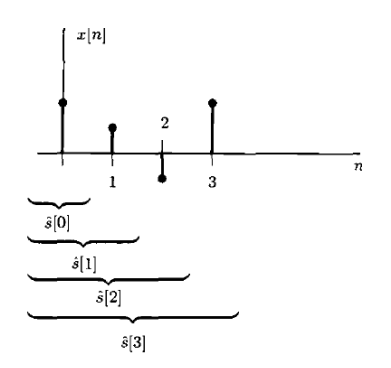

利用 LMMSE 可得

$$ \hat{s}[n]=r_{ss}^{'T}\left(\mathbf{R}_{ss}+\mathbf{R}_{ww}\right)^{-1}\boldsymbol{x} $$

从而得到维纳-霍夫滤波方程

$$ \begin{bmatrix}r_{xx}\begin{bmatrix}0\end{bmatrix}&r_{xx}\begin{bmatrix}1\end{bmatrix}&\cdots&r_{xx}\begin{bmatrix}n\end{bmatrix}\\r_{xx}\begin{bmatrix}1\end{bmatrix}&r_{xx}\begin{bmatrix}0\end{bmatrix}&\cdots&r_{xx}\begin{bmatrix}n-1\end{bmatrix}\\\vdots&\vdots&\ddots&\vdots\\r_{xx}\begin{bmatrix}n\end{bmatrix}&r_{xx}\begin{bmatrix}n-1\end{bmatrix}&\cdots&r_{xx}\begin{bmatrix}0\end{bmatrix}\end{bmatrix}\begin{bmatrix}h^{(n)}\begin{bmatrix}0\end{bmatrix}\\h^{(n)}\begin{bmatrix}1\end{bmatrix}\\\vdots\\h^{(n)}\begin{bmatrix}n\end{bmatrix}\end{bmatrix}=\begin{bmatrix}r_{ss}\begin{bmatrix}0\end{bmatrix}\\r_{ss}\begin{bmatrix}1\end{bmatrix}\\\vdots\\r_{ss}\begin{bmatrix}n\end{bmatrix}\end{bmatrix} $$

### 平滑

$$ \theta=s[n]\text{用 }...,x[-1],x[0],x[1],x[2],...,\text{来估计} $$


LMMSE:

$$ \hat{s}[n]=\sum_{k=-\infty}^\infty a_kx[k] $$

令 $h[k] = a_{N-k}$

正交原理：误差与每一个观测数据正交

$$ E\left(\left(\theta-\hat{\theta}\right)x[m]\right)=0 $$

正交原理不依赖于任务是平滑、滤波还是预测，是普遍适用的，证明如下：   在 LMMSE

$$ \hat{s}[n]=\sum_{k=-\infty}^\infty a_kx[k] $$

中令 $h[k]=a_{n-k}$

则有

$$ \hat s[n] = \sum\limits_{k=-\infty}^{\infty}h[k]x[n-k] $$

可得

$$ r_{ss}\begin{bmatrix}n\end{bmatrix}=h\begin{bmatrix}n\end{bmatrix}*r_{xx}\begin{bmatrix}n\end{bmatrix} $$

无限维纳平滑器的频率响应

$$ H\left(f\right)=\frac{P_{ss}\left(f\right)}{P_{xx}\left(f\right)}\quad=\frac{P_{ss}\left(f\right)}{P_{ss}\left(f\right)+P_{ww}\left(f\right)}\quad=\frac{\eta\left(f\right)}{\eta\left(f\right)+1}\quad\text{,其中 }\eta\left(f\right)=\frac{P_{ss}\left(f\right)}{P_{ww}\left(f\right)} $$

### 预测

可以用来进行预测

$$ \theta=x[N-1+l]\text{ 用 }x[0],x[1],x[2],...,x[N-1]\text{ 来估计} $$


依然用 LMMSE 可以得到线性预测维纳-霍夫滤波方程

$$ \begin{bmatrix}r_{xx}\begin{bmatrix}0\end{bmatrix}&r_{xx}\begin{bmatrix}1\end{bmatrix}&\cdots&r_{xx}\begin{bmatrix}N-1\end{bmatrix}\\r_{xx}\begin{bmatrix}1\end{bmatrix}&r_{xx}\begin{bmatrix}0\end{bmatrix}&\cdots&r_{xx}\begin{bmatrix}N-2\end{bmatrix}\\\vdots&\vdots&\ddots&\vdots\\r_{xx}\begin{bmatrix}N-1\end{bmatrix}&r_{xx}\begin{bmatrix}N-2\end{bmatrix}&\cdots&r_{xx}\begin{bmatrix}0\end{bmatrix}\end{bmatrix}\begin{bmatrix}h\begin{bmatrix}1\end{bmatrix}\\h\begin{bmatrix}2\end{bmatrix}\\\vdots\\h\begin{bmatrix}N\end{bmatrix}\end{bmatrix}=\begin{bmatrix}r_{xx}\begin{bmatrix}l\end{bmatrix}\\r_{xx}\begin{bmatrix}l+1\end{bmatrix}\\\vdots\\r_{xx}\begin{bmatrix}N-1+l\end{bmatrix}\end{bmatrix} $$

### 应用

信道均衡问题

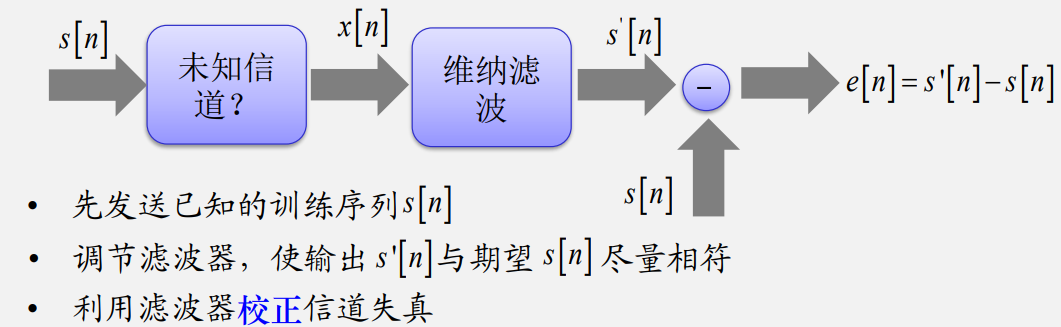
卡尔曼滤波

如何估计电压？

模型 1：当成确定参数

$$ x[n] = A + w[n], w[n] \sim N(0, \sigma^{2}) $$

$$ \hat A = \sum\limits_{n=0}^{N - 1}x[n] = \bar x $$

### 模型2：当成某个随机变量

$$ x[n] = A + w[n], w[n] \sim N(0, \sigma^{2}), A \sim N(\mu_A, \sigma_A^{2}) $$

贝叶斯一般线性模型：

$$ \boldsymbol{x}=\mathbf{H}\boldsymbol{\theta}+\boldsymbol{w}\quad\text{其中 }\boldsymbol{\theta}{\sim}N\begin{pmatrix}\boldsymbol{\mu}_\theta,\mathbf{C}_\theta\end{pmatrix}\text{,}\boldsymbol{w}{\sim}N\begin{pmatrix}\boldsymbol{0},\mathbf{C}_w\end{pmatrix}\\ E\left(\boldsymbol{\theta}\mid\boldsymbol{x}\right)=E\left(\boldsymbol{\theta}\right)+\mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\left(\boldsymbol{x}-E\left(\boldsymbol{x}\right)\right)=\boldsymbol{\mu}_\theta+\mathbf{C}_{\theta|x}\mathbf{H}^T\mathbf{C}_w^{-1}\left(\boldsymbol{x}-\mathbf{H}\boldsymbol{\mu}_\theta\right)\\ \text{其中,}\mathbf{C}_{\theta|x}=\left(\mathbf{C}_\theta^{-1}+\mathbf{H}^T\mathbf{C}_w^{-1}\mathbf{H}\right)^{-1} $$

$$ \hat{A}=\mu_A+\frac{\frac1{\sigma^2/N}}{\frac1{\sigma_A^2}+\frac1{\sigma^2/N}}(\overline{x}-\mu_A) $$

### 模型3：当成未知且随时间变化的量

$$ x[n]=A[n]+w[n],n=0,1,...,N-1 $$

$$ \mathrm{MVU}\text{估计量:}\hat{\boldsymbol{\theta}}=\left(\mathbf{H}^T\mathbf{H}\right)^{-1}\mathbf{H}^T\boldsymbol{x}\\ \begin{aligned}&\boldsymbol{\theta}=&\begin{bmatrix}A[0],A[1],...,A[N-1]\end{bmatrix}^T\\&\mathbf{H}=\mathbf{I}\end{aligned}\\ \hat{A}[n]=x[n] $$

### 动态信号模型

一阶高斯-马尔可夫信号模型：

$$ s[n]=as[n-1]+u[n],n\geq0 $$

其中，$u[n]$是均值为零方差为 $\sigma_u^2$ 的高斯白噪声，称为驱动噪声或激励噪声。信号初值s$[-1]\sim N(\mu_s,\sigma_s^2)$与激励噪声$u[n]$相互独立。

均值：

$$ s[n]=a^{n+1}s[-1]+\sum_{k=0}^na^ku[n-k]\\ E\left(s[n]\right)=a^{n+1}E\left(s[-1]\right)+\sum_{k=0}^na^kE\left(u[n-k]\right)=a^{n+1}\mu_s\\ c_s[m,n] = a^{m+n+2}\sigma_s^2+\sum_{k=0}^m\sum_{l=0}^na^{k+l}E\left(u[m-k]u[n-l]\right)\\ E\left(u[m-k]u[n-l]\right)=\begin{cases}\sigma_u^2,&l=n-m+k\\0,&\mathrm{others}\end{cases} $$

协方差：

$$ m \ge n, c_s\left[m,n\right]=a^{m+n+2}\sigma_s^2+\sum_{k=m-n}^ma^{2k+n-m}\sigma_u^2=a^{m+n+2}\sigma_s^2+\sigma_u^2a^{m-n}\sum_{k=0}^na^{2k}\\ m \lt n, c_s\begin{bmatrix}m,n\end{bmatrix}=a^{m+n+2}\sigma_s^2+\sum_{k=0}^ma^{2k+n-m}\sigma_u^2=a^{m+n+2}\sigma_s^2+\sigma_u^2a^{n-m}\sum_{k=0}^ma^{2k}=c_s\begin{bmatrix}n,m\end{bmatrix} $$

方差和二阶矩：

$$ \begin{aligned} \operatorname{var}(s[n])& =E\left(\left(s[n]-E\left(s[n]\right)\right)\left(s[n]-E\left(s[n]\right)\right)\right) \\ &=c_s[n,n] \\ &=a^{2n+2}\sigma_s^2+\sigma_u^2\sum_{k=0}^na^{2k} \end{aligned}\\ \text{当 }m\geq n\text{ 时}\\r_{ss}\left[m,n\right]=a^{m+n+2}\left(\mu_{s}^{2}+\sigma_{s}^{2}\right)+\sigma_{u}^{2}a^{m-n}\sum_{k=0}^{n}a^{2k}\\\text{当 }m #### 平稳性

$$ \begin{aligned}&E\left(s\left[n\right]\right)=a^{n+1}\mu_s\\&r_{ss}\left[m,n\right]=a^{m+n+2}\left(\mu_s^2+\sigma_s^2\right)+\sigma_u^2a^{m-n}\sum_{k=0}^na^{2k}\end{aligned} $$

不是宽平稳的。

通常要求 $|a| \lt 1$，当取 $n \rarr \infty$ 时

$$ \begin{aligned}&E\left(s\left[n\right]\right)=0\\&r_{ss}\left[m,n\right]=a^{m+n+2}\left(\mu_s^2+\sigma_s^2\right)+\sigma_u^2a^{m-n}\frac{1-a^{2n+2}}{1-a^2}=\frac{\sigma_u^2a^{m-n}}{1-a^2}=r_{ss}\left[k\right]\end{aligned} $$

此时是宽平稳（WSS）的。

递推特性

$$ E\left(s[n]\right)=aE\left(s[n-1]\right)+E\left(u[n]\right)=aE\left(s[n-1]\right) $$

$$ \operatorname{var}\left(s[n]\right)=E\left(\left(s[n]-E(s[n])\right)\left(s[n]-E(s[n])\right)\right) = a^2\operatorname{var}\left(s[n-1]\right)+\sigma_u^2 $$

$$ m \ge n, c_s\left[m,n\right]=a^{m-n}\operatorname{var}\left(s[n]\right) = a^{m-n}\left(a^{2n+2}\sigma_s^2+\sigma_u^2\sum_{k=0}^na^{2k}\right)\\ m \le n, c_s\left[m,n\right]=c_s\left[n,m\right]=a^{n-m}\operatorname{var}\left(s\left[m\right]\right) $$

### 卡尔曼滤波

状态方程：$s[n]=as\left[n-1\right]+u\left[n\right]$

观测方程：$x[n]=s\left[n\right]+w[n]$

驱动噪声 $u[n]$ 相互独立且 $u[n] \sim N(0, \sigma^2)$，观测噪声 $w[n]$ 相互独立且 $w[n] \sim N(0, \sigma^2)$，起始条件 $s[-1] \sim N(0, \sigma_s^2)$。假定 $s[-1], u[n], w[n]$ 之间相互独立。

• 提高估计性能：利用待估计参数的内在联系提高性能
• 减小运算量：通过“老”估计量更新得到“新”估计量

性质：

对联合高斯独立数据矢量可加性：

若$\theta,x_1,x_2$是联合高斯的，数据矢量$x_1,x_2$ 相互独立，则MMSE估计量为：

$$ \hat{\theta}=E\left(\boldsymbol{\theta}\right)+\mathbf{C}_{\theta x_1}\mathbf{C}_{x_1x_1}^{-1}\left(\boldsymbol{x}_1-E\left(\boldsymbol{x}_1\right)\right)+\mathbf{C}_{\theta x_2}\mathbf{C}_{x_2x_2}^{-1}\left(\boldsymbol{x}_2-E\left(\boldsymbol{x}_2\right)\right) $$

对待估计参数的可加性：

若 $\boldsymbol{\theta}=\boldsymbol{\theta}_1+\boldsymbol{\theta}_2$, 则相应的MMSE估计量是可加的，即

$$ \hat{\theta}=E\left(\boldsymbol{\theta}\mid\boldsymbol{x}\right)=E\left(\boldsymbol{\theta}_1+\boldsymbol{\theta}_2\mid\boldsymbol{x}\right)=E\left(\boldsymbol{\theta}_1\mid\boldsymbol{x}\right)+E\left(\boldsymbol{\theta}_2\mid\boldsymbol{x}\right) $$

线性变换的不变性：

若$\alpha=\mathbf{A\theta}+\boldsymbol{b},\quad\theta$ 的MMSE估计量是 $\theta$, 则 $\alpha$ 的MMSE估计量为：

$$ \hat{\alpha}=\mathbf{A}\hat{\theta}+b $$

定义：

$$ \hat{s}[n-1]=E\left(s[n-1]|x[0],x[1],...,x[n-1]\right)\triangleq\hat{s}[n-1\mid n-1]\\ M\begin{bmatrix}n-1\end{bmatrix}=E\left(\left(s\begin{bmatrix}n-1\end{bmatrix}-\hat{s}\begin{bmatrix}n-1\end{bmatrix}\right)^2\right)\\ \hat s[n] \triangleq\hat{s}[n\mid n] $$

其中，前面的 n 表示被估计的信号下表，后面的 n 表示估计量用到的数据中最新的那个数据的下标。

如果能够提取出第 n 个数据点带来的新的信息，并加入之前已有的估计量，就可更新估计量：

$$ \begin{aligned} \hat{s}\Big[n|n\Big]& =E\left(s[n]|x[0],x[1],...,x[n-1],x[n]\right) \\ &=E\left(s[n]|x[0],x[1],...,x[n-1],\tilde{x}[n]\right) \\ &=\underbrace{E\left(s[n]|x[0],x[1],...,x[n-1]\right)}_{先前数据估计}+\underbrace{E\left(s[n]|\tilde{x}[n]\right)}_{新息估计} \end{aligned} $$

新息与已有的数据正交。

$$ \tilde{x}[n]=x[n]-\hat{x}[n|n-1] $$

“先前数据估计”怎么求解？

$$ \begin{aligned} \hat{s}[n\mid n-1]& =E\left(as[n-1]+u[n]|x[0],x[1],...,x[n-1]\right) \\ &=E\left(as[n-1]|x[0],x[1],...,x[n-1]\right)+E\left(u[n]|x[0],x[1],...,x[n-1]\right) \\ &=aE\left(s\begin{bmatrix}n-1\end{bmatrix}|x\begin{bmatrix}0\end{bmatrix},x\begin{bmatrix}1\end{bmatrix},...,x\begin{bmatrix}n-1\end{bmatrix}\right)\\ &=a\hat{s}\begin{bmatrix}n-1|n-1\end{bmatrix} \\ \end{aligned} $$

#### 预测

求解新息

$$ E\left(s[n]|\tilde{x}[n]\right)=E\left(s[n]\right)+\mathbf{C}_{s\tilde{x}}\mathbf{C}_{\tilde{x}\tilde{x}}^{-1}\left(\tilde{x}[n]-E\left(\tilde{x}[n]\right)\right) $$

$$ s[n]=a^{n+1}s[-1]+\sum_{k=0}^na^ku[n-k]\rArr E(s[n]) = 0\\ $$

$$ \begin{gathered} E\left(\tilde{x}[n]\right)=E\left(x[n]-\hat{x}[n\mid n-1]\right) \\ E\left(x[n]\right)=E\left(s[n]+w[n]\right)=0 \\ E\left(\hat{x}[n\mid n-1]\right)=E\left(\sum_{k=0}^{n-1}a[k]x[k]\right) \end{gathered}\\ \rArr E\left(\hat{x}[n\mid n-1]\right)=0\\ \rArr E(\tilde x[n]) = 0 $$

因此，

$$ E\left(s[n]|\tilde{x}[n]\right)=\mathbf{C}_{s\tilde{x}}\mathbf{C}_{\tilde{x}\tilde{x}}^{-1}\tilde{x}[n]=\underbrace{\mathbf{C}_{s\tilde{x}}\mathbf{C}_{\tilde{x}\tilde{x}}^{-1}}_{卡尔曼增益}\left(x[n]-\hat{x}[n\mid n-1]\right) $$

#### 最小预测 MSE

$\mathbf{C}_{s\tilde{x}}\text{的求解}$

$$ \begin{aligned} C_{s\tilde{x}}& =E\left(s[n]\tilde{x}[n]\right) \\ &=E\Big(s[n]\Big(x[n]-\hat{x}\Big[n|n-1\Big]\Big)\Big) \end{aligned} $$

其中

$$ \begin{aligned}\hat{x}\left[n|n-1\right]&=E\left(x[n]|x[0],x[1],...x[n-1]\right)=E\left(s[n]+w[n]|x[0],x[1],...x[n-1]\right)\\&=E\left(s[n]|x[0],x[1],...x[n-1]\right)=\hat{s}\left[n|n-1\right]\end{aligned} $$

因此

$$ \begin{aligned} C_{s\tilde{x}}& =E\left(s[n]\left(s[n]+w[n]-\hat{s}[n|n-1]\right)\right) \\ &=E\left(s[n]w[n]+s[n]\left(s[n]-\hat{s}[n|n-1]\right)\right) \\ &=E\Big(s[n]\Big(s[n]-\hat{s}\Big[n|n-1\Big]\Big)\Big)\\ &=E\left(s[n]\left(s[n]-\hat{s}[n|n-1]\right)\right)-E\left(\hat{s}[n|n-1]\left(s[n]-\hat{s}[n|n-1]\right)\right)\\ &=E\left(\left(s[n]-\hat{s}[n|n-1]\right)\left(s[n]-\hat{s}[n|n-1]\right)\right)\\ &\triangleq M\begin{bmatrix}n\mid n-1\end{bmatrix} \end{aligned} $$

求解 $M\begin{bmatrix}n\mid n-1\end{bmatrix}$

$$ \begin{aligned} &M\begin{bmatrix}n\mid n-1\end{bmatrix}\\ &=E\left(\left(as\begin{bmatrix}n-1\end{bmatrix}+u\begin{bmatrix}n\end{bmatrix}-\hat{s}\begin{bmatrix}n|n-1\end{bmatrix}\right)^2\right)\\ &=E\left(\left(a\left(s[n-1]-\hat{s}[n-1\mid n-1]\right)+u[n]\right)^2\right) \\ &=E\left(a^2\left(s\left[n-1\right]-\hat{s}\left[n-1\mid n-1\right]\right)^2+u^2\left[n\right]+2a\left(s\left[n-1\right]-\hat{s}\left[n-1\mid n-1\right]\right)u\left[n\right]\right) \\ &=a^2M\left[n-1\mid n-1\right]+\sigma_u^2 \end{aligned} $$

#### 卡尔曼增益

$\mathbf{C}_{\tilde{x}\tilde{x}}\text{的求解}$

$$ \\ \begin{aligned} \mathbf{C}_{\tilde{x}\tilde{x}}&=E\left(\left(\tilde{x}[n]-E(\tilde{x}[n])\right)^2\right) = E\left(\tilde{x}^2[n]\right) = E\left(\left(x[n]-\hat{s}[n\mid n-1]\right)^2\right)\\ &=E\left(\left(s[n]+w[n]-\hat{s}[n\mid n-1]\right)^2\right) \\ &=E\left(\left(s[n]-\hat{s}[n\mid n-1]\right)^2+w^2\left[n\right]+2\left(s[n]-\hat{s}[n\mid n-1]\right)w[n]\right) \\ &=M\begin{bmatrix}n\mid n-1\end{bmatrix}+\sigma_n^2 \end{aligned} $$

结合

$$ \begin{aligned}\mathbf{C}_{\tilde{x}\tilde{x}}&=M\begin{bmatrix}n\mid n-1\end{bmatrix}+\sigma_n^2\\\mathbf{C}_{s\tilde{x}}&=M\begin{bmatrix}n\mid n-1\end{bmatrix}\end{aligned} $$

我们得到了卡尔曼增益

$$ E\left(s[n]|\tilde{x}[n]\right)=\underbrace{\frac{M\left[n\mid n-1\right]}{M\left[n\mid n-1\right]+\sigma_n^2}}_{卡尔曼增益 K[n]}\tilde{x}[n] $$

#### 修正

$$ \hat{s}\left[n\mid n\right]=\underbrace{\hat{s}\left[n\mid n-1\right]}_{预测}+\underbrace{K\left[n\right]\left(x\left[n\right]-\hat{s}\left[n\mid n-1\right]\right)}_{新息修正} $$

#### 最小 MSE

MSE 修正：

$$ M[n|n] = (1 - K[n])M[n|n - 1] $$

### 非零均值信号模型

初始化：$\hat{s} [ - 1|- 1] = E\begin{pmatrix} s[ - 1] \end{pmatrix} = \mu _s$ $M[ - 1|- 1] = E\left ( \begin{pmatrix} s[ - 1] - \hat{s} [ - 1|- 1] \end{pmatrix} ^2\right ) = \sigma _s^2$

估计量预测：$\hat{s}[n|n-1]=a\hat{s}[n-1|n-1]$

MSE预测：$M\left[n\mid n-1\right]=a^2M\left[n-1\mid n-1\right]+\sigma_u^2$

卡尔曼增益：$K[n]=\frac{M\left[n|n-1\right]}{M\left[n|n-1\right]+\sigma_n^2}$

估计量修正：$\hat{s}[n|n]=\hat{s}[n|n-1]+K[n]\left(x[n]-\hat{s}[n|n-1]\right)$

MSE修正: $M\left [ n\mid n\right ] = \left ( 1- K\left [ n\right ] \right ) M\left [ n\mid n- 1\right ]$

矢量状态-标量观测信号模型

矢量状态-矢量观测信号模型

非线性信号模型

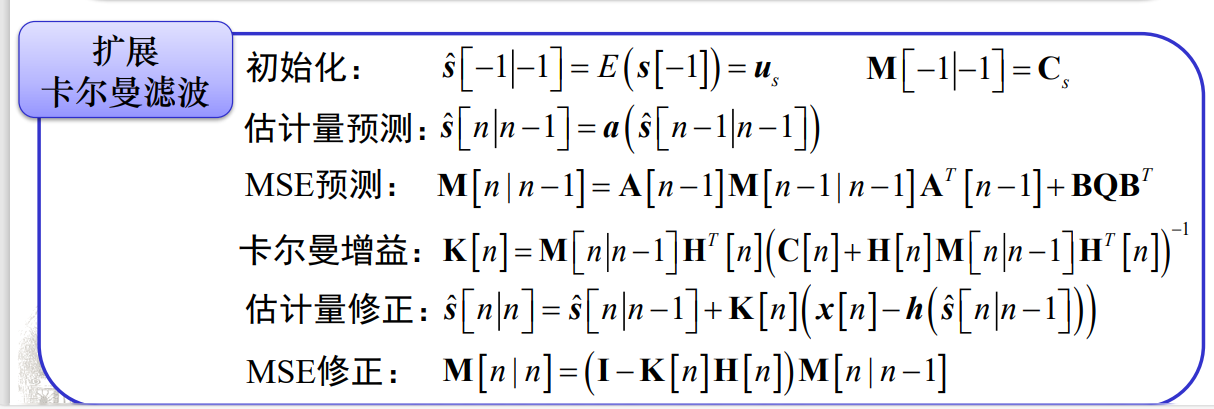
总结

• 不同时刻的待估计参数并不完全一样，但是存在某些内在联系
• 卡尔曼滤波利用这种联系进行 LMMSE 估计，并减少了运算量
• 如果信号与噪声是高斯的，则卡尔曼滤波在 MMSE 准则下最佳，否则，在 LMMSE 准则下是最佳的。

信号检测基本准则与方法

之前一直在研究连续型的问题（回归/估计），这里研究离散型的问题（分类/检测）。

Neyman-Pearson 准则

适用于没有先验信息、代价不好量化的场景。

两种假设：

$$ \begin{aligned}&H_0:x[n]=w[n],n=0,1,...,N-1\\&H_1:x[n]=s[n]+w[n],n=0,1,...,N-1\end{aligned} $$

$$ \begin{aligned} &P\left(H_1;H_0\right):\text{ 虚警概率}\left(P_{FA},\text{有时简记为}P_F\right)\\ &P\left(H_0;H_1\right):\text{ 漏检概率 }\left(P_M\right)\\ &P\left(H_1;H_1\right):\text{ 检测概率 }\left(P_D\right)\end{aligned} $$

要求：在虚警概率一定情况下，使检测概率最大化

检测概率和虚警概率之间追求折中，不可能两者都改善。

对给定的虚警概率 $P_{FA}=\alpha$ ,使检测概率 $P_D$ 最大的判决为

$$ L(x)=\frac{p(x;H_1)}{p(x;H_0)}>\gamma $$

其中门限由 $P_{FA}=\int_{\lbrace\mathbf{x}:L(\mathbf{x})>\gamma\rbrace}p(\boldsymbol{x};H_0)d\boldsymbol{x}=\alpha$ 决定

对于信号检测问题：

$$ H_0:\boldsymbol{x}\sim N\left(\boldsymbol{0},\sigma^2\mathbf{I}\right)\\H_1:\boldsymbol{x}\sim N\left(A\mathbf{1},\sigma^2\mathbf{I}\right) $$

NP 检测器：

$$ \frac{p\left(\boldsymbol{x};H_1\right)}{p\left(\boldsymbol{x};H_0\right)}=\frac{\frac1{\left(2\pi\sigma^2\right)^{N/2}}\exp\left\{-\frac1{2\sigma^2}\sum_{n=0}^{N-1}\left(x[n]-A\right)^2\right\}}{\frac1{\left(2\pi\sigma^2\right)^{N/2}}\exp\left\{-\frac1{2\sigma^2}\sum_{n=0}^{N-1}x^2[n]\right\}}>\gamma\\\quad\exp\left\{-\frac1{2\sigma^2}\sum_{n=0}^{N-1}\left(x[n]-A\right)^2+\frac1{2\sigma^2}\sum_{n=0}^{N-1}x^2[n]\right\}>\gamma $$

$$ -\frac1{2\sigma^2}\Bigg(-2A\sum_{n=0}^{N-1}x[n]+NA^2\Bigg)>\ln\gamma\\\frac1N\sum_{n=0}^{N-1}x[n]>\frac{\sigma^2}{NA}\ln\gamma+\frac A2 $$

称为检测统计量。若均值大于门限，则判为有信号，否则为无信号。

使用方法：

$$ \begin{aligned} &\text{检测统计量:}T(x)=\frac1N\sum_{n=0}^{N-1}x[n]\sim\begin{cases}N\Big(0,\sigma^2\Big/_N\Big),&H_0\\[2ex]N\Big(A,\sigma^2\Big/_N\Big),&H_1\end{cases} \\ &\text{虚警概率:}P_{FA}=Pr\left(T\left(\boldsymbol{x}\right)>\gamma^{'};H_0\right)=Q\left(\frac{\gamma^{'}}{\sqrt{\sigma^2/N}}\right) \\ &\text{门限设置:}\gamma^{\prime}=\sqrt{\frac{\sigma^2}N}Q^{-1}\left(P_{FA}\right) \\ & \begin{aligned}&\text{相应的检测概率:}\\&P_{D}=Pr\Big(T\big(\boldsymbol{x}\big)>\gamma^{'};H_{1}\Big)=Q\Bigg(\frac{\gamma^{'}-A}{\sqrt{\sigma^{2}/N}}\Bigg)=Q\Bigg(\frac{\sqrt{\frac{\sigma^{2}}{N}}Q^{-1}\big(P_{FA}\big)-A}{\sqrt{\sigma^{2}/N}}\Bigg)\end{aligned} \\ &=Q\Bigg(Q^{-1}\big(P_{F_A}\big)-\sqrt{\frac{NA^2}{\sigma^2}}\Bigg) \end{aligned} $$

### 检测性能分析

接收机工作特性曲线（ROC, receiver operating characteristics）

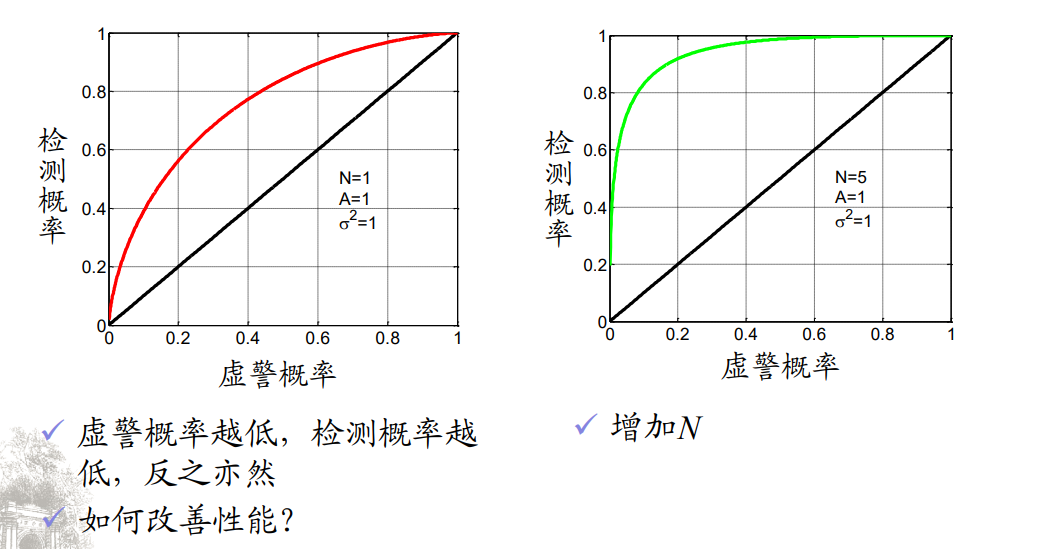
直观理解：

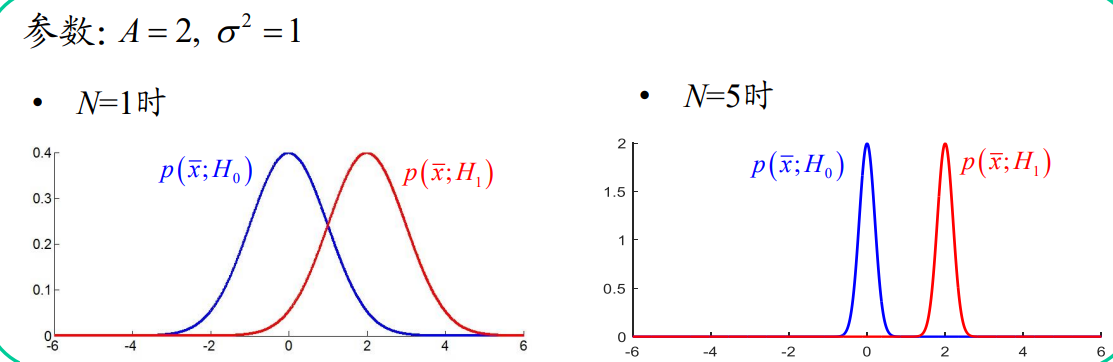
多次观测的好处

• 从数学角度：不同假设下的pdf分隔更开，更易区分不同假设
• 从信号处理角度：增加信号预检测积分时间，获得更多的能量用于检测
• 从信息论角度：多的观测数据带来了新的信息

最小错误概率准则

$$ \begin{aligned} P_{e}& =\Pr\left\{\text{判}H_0,H_1\text{为真}\right\}+\Pr\left\{\text{判}H_1,H_0\text{为真}\right\} \\ &=P\big(H_0,H_1\big)+P\big(H_1,H_0\big) \\ &=P\big(H_1\big)P\big(H_0|H_1\big)+P\big(H_0\big)P\big(H_1|H_0\big) \\ &=P\big(H_1\big)\int_{R_0}p\big(\boldsymbol{x}|H_1\big)d\boldsymbol{x}+P\big(H_0\big)\int_{R_1}p\big(\boldsymbol{x}|H_0\big)d\boldsymbol{x} \\ &=P\big(H_1\big)\Bigg(1-\int_{R_1}p\big(\boldsymbol{x}\mid H_1\big)d\boldsymbol{x}\Bigg)+P\big(H_0\big)\int_{R_1}p\big(\boldsymbol{x}\mid H_0\big)d\boldsymbol{x} \\ &=P\left(H_1\right)+\int_{R_1}\left\{P\left(H_0\right)p\left(\boldsymbol{x}\mid H_0\right)-P\left(H_1\right)p\left(\boldsymbol{x}\mid H_1\right)\right\}d\boldsymbol{x} \end{aligned} $$

为了使错误最小，需要在积分式小于零的区域积分，即

$$ \frac{p\left(\boldsymbol{x}\mid H_1\right)}{p\left(\boldsymbol{x}\mid H_0\right)}>\frac{P\left(H_0\right)}{P\left(H_1\right)}\text{ 时,判 }H_1 $$

最小错误概率准则可推导出最大后验概率检测器：

$$ \frac{p\left(\boldsymbol{x}\mid H_1\right)}{p\left(\boldsymbol{x}\mid H_0\right)}>\frac{P\left(H_0\right)}{P\left(H_1\right)}\text{ 时,判 }H_1 $$

等价于

$$ \frac{p\left(\boldsymbol{x}\mid H_1\right)P\left(H_1\right)}{p\left(\boldsymbol{x}\right)}>\frac{p\left(\boldsymbol{x}\mid H_0\right)P\left(H_0\right)}{p\left(\boldsymbol{x}\right)}\\p\left(H_1\mid\boldsymbol{x}\right)>p\left(H_0\mid\boldsymbol{x}\right) $$

若先验概率相同，则为最大似然检测器：

$$ p\left(x\mid H_1\right)>p\left(x\mid H_0\right) $$

### 二元贝叶斯风险准则

引入判错代价

$$ R=C_{01}P\left(H_1\right)P\left(H_0\mid H_1\right)+C_{10}P\left(H_0\right)P\left(H_1\mid H_0\right) $$

进一步泛化：

$$ R=C_{00}P\big(H_0\big)P\big(H_0|H_0\big)+C_{10}P\big(H_0\big)P\big(H_1|H_0\big)\\+C_{01}P\big(H_1\big)P\big(H_0|H_1\big)+C_{11}P\big(H_1\big)P\big(H_1|H_1\big) $$

$$ \begin{aligned}\text{R}&=C_{00}P\left(H_0\right)+C_{01}P\left(H_1\right)\\&+\int_{R_1}\left\{\left(C_{10}-C_{00}\right)P\left(H_0\right)p\left(\boldsymbol{x}\mid H_0\right)-\left(C_{01}-C_{11}\right)P\left(H_1\right)p\left(\boldsymbol{x}\mid H_1\right)\right\}d\boldsymbol{x}\end{aligned} $$

因此，有了最小贝叶斯风险判决准则：

$$ \frac{p\left(\boldsymbol{x}\mid H_1\right)}{p\left(\boldsymbol{x}\mid H_0\right)}>\frac{\left(C_{10}-C_{00}\right)P\left(H_0\right)}{\left(C_{01}-C_{11}\right)P\left(H_1\right)}\text{ 时,判 }H_1 $$

风险一致条件下（$C_{00}=C_{11}=0,C_{10}=C_{01}=1$），回到最小错误概率准则。

多元贝叶斯风险准则

贝叶斯风险：

$$ \begin{aligned} \text{R}& =\sum_{i=0}^{M-1}\sum_{j=0}^{M-1}C_{ij}P\Big(H_i,H_j\Big) \\ &=\sum_{i=0}^{M-1}\sum_{j=0}^{M-1}C_{ij}\int_{R_i}P\Big(x,H_j\Big)dx \\ &=\sum_{i=0}^{M-1}\int_{R_i}\sum_{j=0}^{M-1}C_{ij}P\Big(x,H_j\Big)dx \\ &=\sum_{i=0}^{M-1}\int_{R_i}\sum_{j=0}^{M-1}C_{ij}P\Big(H_j\mid x\Big)p(x)dx \end{aligned} $$

应选择使平均风险$C_i\left(\boldsymbol{x}\right)=\sum_{j=0}^{M-1}C_{ij}P\left(H_j\mid\boldsymbol{x}\right)$最小的假设

在风险一致条件下

$$ C_{ij}=\begin{cases}0,&i=j\\1,&i\neq j\end{cases} $$

$$ \begin{aligned}C_{i}\left(\boldsymbol{x}\right)&=\sum_{j=0\atop j\neq i}^{M-1}P\Big(H_j\mid\boldsymbol{x}\Big)\\&=\sum_{j=0}^{M-1}P\Big(H_j\mid\boldsymbol{x}\Big)-\underline{P\Big(H_i\mid\boldsymbol{x}\Big)}_{最大化这个}\end{aligned} $$

因此等价于最大后验准则：

$$ \max_iP(H_i\mid\boldsymbol{x}) $$

若此时先验概率相同，则为最大似然准则。

总结知识点

估计理论

MAP 估计通常不能使用参数变换，变换后的参数不一定是 MAP。但是 MLE 可以。

LS 方法与 BLUE 等 MVU 的衍生方法有一点不同，就是基础的 LS 没有使用协方差矩阵，但是加权的 LS 可以用协方差矩阵修正结果。

贝叶斯方法和经典方法的区别在于是否把估计量的真值看作一个随机变量。它们都以“平均误差最小”为目标。

检测理论

贝叶斯风险：让平均的风险最小化。

未知多余参数如果影响最终的判决结果，可以用贝叶斯方法或者GLRT方法处理。