语音信号的线性预测编码技术
线性预测编码技术(维纳滤波)。可以参考隔壁统计信号处理的笔记hh。
维纳滤波的正交原理:
$$ E \langle x(n-k), e(n) \rangle = 0 $$正交原理可以用来估计任何时候的任何值,不管是现在(滤波),过去(平滑)还是未来(预测),也不管估计的对象是 $x,y$ ,上述公式的含义是:估计误差始终与已知信号垂直,与估计的是哪个时间的信号无关。
利用前面的 $P$ 个信号预测下一个信号:
$$ \hat{s}(n)=-\sum_{i=1}^{P^{\prime}}\hat{\alpha}_i\cdot s(n-i) $$误差定义为
$$ \begin{aligned} \varepsilon(n)& =s(n)-\overset{\wedge}{\operatorname*{s}}(n)=s(n)+\sum_{i=1}\widehat{\alpha}_i\cdot s(n-i) \\ &=\sum_{i=0}^{P^{\prime}}\widehat{\alpha}_i\cdot s(n-i) \end{aligned} $$从 z 域看,这是一个全极点模型产生了目标信号:
$$ S(z) = -S(z)\sum\limits_{i=1}^{P}\alpha_iz^{-i} + E(z) $$接下来的所有步骤,目的都是推导 $\alpha$ 的取值。
自相关法
本文中假设信号具有遍历性,即时间平均等于统计平均,时间上的自相关等于统计意义上的自相关。
利用 LMMSE 准则可以推出
$$ \begin{bmatrix}R(0)&R(1)&R(2)&\cdots&R(P-1)\\R(1)&R(0)&R(1)&\cdots&R(P-2)\\R(2)&R(1)&R(0)&\cdots&R(P-3)\\\vdots&\vdots&&&\vdots\\R(P-1)&R(P-2)&\cdots&\cdots&R(0)\end{bmatrix}\cdot\begin{bmatrix}\hat\alpha_1\\\hat\alpha_2\\\vdots\\\vdots\\\hat\alpha_P\end{bmatrix}=-\begin{bmatrix}R(1)\\R(2)\\\vdots\\\vdots\\R(P)\end{bmatrix} $$一个例子:Durbin 递推算法
协方差法
不能保证声码器稳定
Durbin 递推算法
滤波器的内积
定义 $s_w(n)$ 关于 $F(z)$ 和 $G(z)$ 的内积如下:
$$ \langle F(z),G(z)\rangle=\sum_{-\infty}^{+\infty}u(n)\cdot v(n) $$特别地若这里的 $F(z),\quad G(z)$ 都用我们的逆滤波器 $A(z)=\sum_{i=0}^P\alpha_iZ^{-i}$ 替换,那么语音信号 $s_w(n)$ 经过 $A(z)$ 后的输出 $e(n)$ 就是预测误差。
$\alpha_i\cdot s_W(n-i)$ 因此 $A(z)$ 范数 $\|A(z)\|$ 的平方就是预测误差。即 $$ \|A(z)\|^2=\langle A(z),A(z)\rangle=\sum_{-\infty}^{+\infty}e(n)\cdot e(n)=\sum_{-\infty}^{+\infty}e^2(n) $$内积有正定性,线性,三角不等式
特殊性质:
$$ \langle z^{-i}, z^{-j} \rangle = R(|i - j|)\\ \langle F(z), G(z) \rangle = \sum\limits_{i=0}^{M}\sum\limits_{j=0}^{M}f_ig_jR(|i - j|)\\ \langle F(z),G(z)\rangle=\left\langle z^kF(z),z^kG(z)\right\rangle\\ \langle F(z),G(z)\rangle=\langle F(1/z),G(1/z)\rangle $$逆滤波器
定义FIR滤波器 $\hat{A}(z)$ :
$$ \hat{A}(z)=\sum_{i=0}^P\hat{\alpha}_iz^{-i}\quad,\quad\alpha_0=1 $$若 $\hat{\alpha}_{i}$ 是满足LPC正则方程的解,则称 $\hat{A}(z)$ 称为逆滤波器。 $\hat{E}(z)=\hat{A}(z)\cdot S(z)$ 是预测误差 $\varepsilon(n)$ 的z 变换。显然有:
(1) 若s(n)是由全极点模型 $1/A(z)$ 产生的,这时 $A(z)=\sum_{i=0}^P\alpha_iz^{-i}$ , 即:
$s(n)=-\sum_{i=1}^P\alpha_is(n-i)+Ge(n)$ $$ S(z) \cdot A(z) = G \cdot E(z) $$前向和后向预测
前向线性预测器(P阶)
$$ \hat{s}(n)=-\sum_{i=1}^P\alpha_i^{(P)}\cdot s(n-i) $$前向预测误差(P阶)
$$ \varepsilon_\alpha^{(P)}(n)=s(n)-\hat{s}(n)=\sum_{i=0}^P\alpha_i^{(P)}\cdot s(n-i)\:,\alpha_0^{(P)}=1 $$前向逆滤波器(P阶)
$$ A^{(P)}(z)=\sum_{i=0}^P\alpha_i^{(P)}z^{-i} $$显然有
$$ E^{(P)}_\alpha(z) = S(z) \cdot A^{(P)}(z) $$后向线性预测器(P阶)
$$ \hat{s}(n-P-1)=-\sum_{i=1}^P\beta_i^{(P)}\cdot s(n-i) $$n时刻对 $s(n-P-1)$ 的后向预测误差(P阶)
$$ \begin{aligned}&\varepsilon_{\beta}^{(P)}(n)=s(n-P-1)-\hat{s}(n-P-1)\\&=\sum_{i=1}^{P+1}\beta_i^{(P)}\cdot s(n-i)\quad,\quad\beta_{P+1}^{(P)}=1\end{aligned} $$后向逆滤波器 (P阶)
$$ B^{(P)}(z)=\sum_{i=1}^{P+1}\beta_i^{(P)}z^{-i} $$显然有
$$ E_\beta^{(P)}(z) = S(z) \cdot B^{(P)}(z) $$正交性原理
判定最佳预测器的充要条件是
$$ \langle A^{(m)}(z), z^{-l} \rangle = 0\\ \langle B^{(m)}(z), z^{-l} \rangle = 0\\ l = 1, 2, \dots, m $$一个不严谨的理解:
$$ u(n) = s(n) * Z^{-1}[A(z)] = \varepsilon(n)\\ v(n) = s(n) * Z^{-1}[z^{-l}] = s(n - l)\\ \begin{align*} &\langle A^{(m)}(z), z^{-l} \rangle\\ =&\sum\limits_{n=-\infty}^{\infty}u(n)v(n)\\ =&\sum\limits_{n=-\infty}^{\infty}\varepsilon(n)s(n - l)\\ \end{align*} $$由于时间平均等于统计平均,
$$ \frac1{2N} \sum\limits_{n=-N}^{N - 1}\varepsilon(n)s(n-l) = E \langle \varepsilon(n), s(n-l) \rangle $$根据开头提到的维纳滤波正交原理可知上式等于0。
递推公式
根据定义,当 $m=0$ 时,显然有
$$ A^{(0)}(z)=1\\B^{(0)}(z)=z^{-1} $$ $m>0$ 时有如下递推公式(施密特正交化) $$ A^{(m)}(z)=A^{(m-1)}(z)+K^{(m)}B^{(m-1)}(z) $$ $$ B^{(m)}(z)=z^{-1}\Big[B^{(m-1)}(z)+K^{(m)}A^{(m-1)}(z)\Big] $$ $$ K^{(m)} = -\frac{\langle A^{(m-1)}(z), B^{(m-1)}(z)\rangle}{||B^{(m-1)}(z)||^2} $$根据正交性原理,需要证明由递推公式得到的 $A^{(m)}(z)$ 和 $B^{(m)}(z)$ 满足正交性条件公式。
在公式(76) 中,根据多项式对应项系数相等的原则,可以得到
$$ \begin{aligned}&\alpha_{i}^{(m)}=\alpha_{i}^{(m-1)}+K^{(m)}\cdot\beta_{i}^{(m-1)}\quad,\quad i=1,\cdots,m-1\\&\alpha_{i}^{(m)}=K^{(m)}\quad,\quad i=m\end{aligned} $$由公式(73)可知
$$ \beta_j^{(m)}=\alpha_{m+1-j}^{(m)},\:j=1,\cdots,m+1 $$从这里可以推出
$$ > B^{(m)}(z) = z^{-(m+1)}A^{(m)}(1/z) > $$
因此可以得到预测器系数的递推公式
$$ \begin{cases}\alpha_\mathrm{m}^{(\mathrm{m})}=\mathrm{K}^{(\mathrm{m})}\\\alpha_\mathrm{i}^{(\mathrm{m})}=\alpha_\mathrm{i}^{(\mathrm{m}-1)}+\mathrm{K}^{(\mathrm{m})}\cdot\alpha_\mathrm{m-i}^{(\mathrm{m}-1)}\quad,\:\mathrm{i}=1,\cdots,\mathrm{m}-1\end{cases} $$这是线性预测系数的Durbin递推算法公式。 $m$ 阶部分相关系数 $K^{(m)}$ 可以用以下方法计算:
$$ K^{(m)} = -\frac{\sum\limits_{j=1}^{m}\alpha_{m-j}^{(m-1)}R(j)}{||B^{(m-1)}(z)||^2} $$ $||B^{(m)}(z)||^2$ 可以用这个递推式计算: $$ \begin{Vmatrix}B^{(m)}(z)\end{Vmatrix}^2=(1-[K^{(m)}]^2)\begin{Vmatrix}B^{(m-1)}(z)\end{Vmatrix}^2 $$初值
$$ ||B^{(0)}(z)|| = R(0)\\ \alpha^{(0)}_0 = 1 $$Durbin 算法系统的稳定性
充分性:
$$ \frac{1}{A^{(m)}(z)} 稳定 \Rarr |k^{(m)}| < 1 $$必要性:
$$ |k^{(m)}| < 1 \Rarr \frac{1}{A^{(m)}(z)} 稳定 $$Highlight:
Durbin 逆序递推公式
$$ A^{(m-1)}(z)=\frac{A^{(m)}(z)-k^{(m)}zB^{(m)}(z)}{1-(k^{(m)})^2} $$证明过程中引入的一个辅助函数
$$ F^{(m)}(z)=\frac{A^{(m)}(z)}{zB^{(m)}(z)}=\frac{z^mA^{(m)}(z)}{A^{(m)}(1/z)} $$满足 $F^{(m)}(z) < 1 \lrArr |z| < 1$
稳定性的应用
充分性:说明使用 Durbin 算法可以保证 $1/A(z)$ 稳定
必要性:
判定高阶多项式 $A(z)$ 构成的系统 $1/A(z)$ 是否稳定。
只要计算出 $k_m$ ,判断 $|k_m|$ 是否小于1即可。
LPC 模型参数讨论
阶数
误差能量是单调减的,一般 $P = 8 \sim 14$
激励增益 G
采用缓变窗(哈明窗), $N >> P$
$$ \varepsilon_\alpha^{(p)}(n)\approx Ge_w(n)=Ge(n)w(n) $$ $$ G^2\approx\frac{\sum_{n=-\infty}^\infty\left(\varepsilon_\alpha^{(p)}(n)\right)^2}{\sum_{n=-\infty}^\infty e^2(n)w^2(n)} $$短时分析对于LPC参数估计的影响
- 𝑒(𝑛)为白噪声时, $E[\hat \alpha_i] = \alpha_i$ ,无偏估计
- 𝑒(𝑛)为浊音时,采用基音同步算法可以达到无偏估计。否则如果是任意截取一段语音作分析估计是有偏的。
LPC分析的频域解释
用LPC分析可以用来跟踪声道模型谱(或称语音的平滑谱)。若用LPC算法解出的全极点模型来逼近实际声道,则它的单位冲激响应ℎ(𝑛)为:
$$ \begin{cases} h(n) = 0, n \lt 0\\ h(n) = - \sum\limits_{i=1}^{p}\alpha_i^{(p)}h(n - 1) + \delta(n), n \ge 0 \end{cases} $$若 $R_h(l) = R_h(-l) = \sum\limits_{n=0}^{\infty}h(n - l)h(n), l \ge 0$
$$ \sum\limits_{i=1}^{p}\alpha_i^{(P)}R_h(|k - i|) = -R_h(k), l \ge 0\\ R_h(l)/R_h(0) = R(l) / R(0) $$当激励为均方值为1,均值为0的白噪声序列时,输出的自关函数𝑅𝑤(𝑙)也有此关系。
P阶LPC预测模型也称为P阶自关匹配模型。
各种LPC参数计算其它们之间的关系
- $R(l) \Rightarrow \alpha$
- $K \Rightarrow \alpha$
- LPC 系数 => 倒谱(因为是最小相位序列)
- PARCOR 系数( $K^{(m)}$ )
- 由 Durbin 解得
- 由格形算法解得
- 由 Schur 算法解得
- 由 $A(z)$ 根确定振峰
- 每一对根与一个共振峰对应
- 声道面积比系数和对数面积比系数
- 线谱对(LSP)或者线谱频率参数(LSF)
性质:
- $P(z)$ 和 $Q(z)$ 的根均在单位圆上
- $P(z)$ 和 $Q(z)$ 的根在单位元上交错
- $\alpha$ 参数和 $LSP$ 参数互推
某个特定的𝐿𝑆𝑃 [𝑓1, 𝑓2, ⋯ 𝑓𝑝]中只移动其中任意一个频率𝑓𝑖的位置,那么对应的平滑谱只
有𝑓𝑖附近与原平滑谱有异,而在其它频域则变化很小
语音信号编码
语音信号的标量量化
标量量化器
均匀量化器
非均匀量化器
非线性压扩量化器
自适应量化(Adaptive Delta Modulation,ADM)
前向自适应量化(AQF)
后向自适应量化(AQB)
差分编码 DPCM
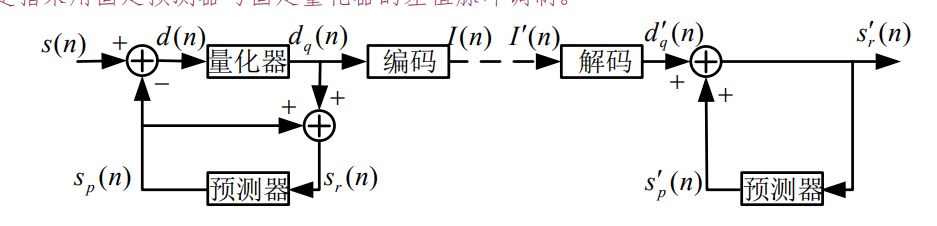
DPCM是指采用固定预测器与固定量化器的差值脉冲调制。
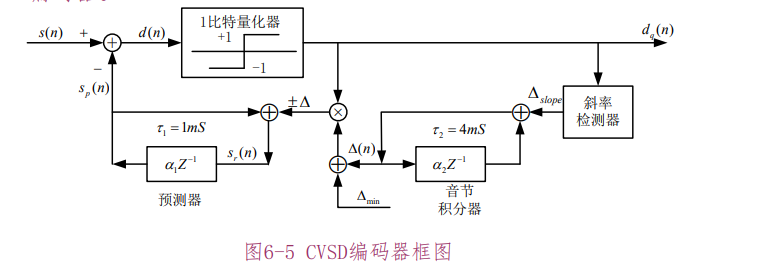
CVSD 编码器
Delta-Sigma 量化器
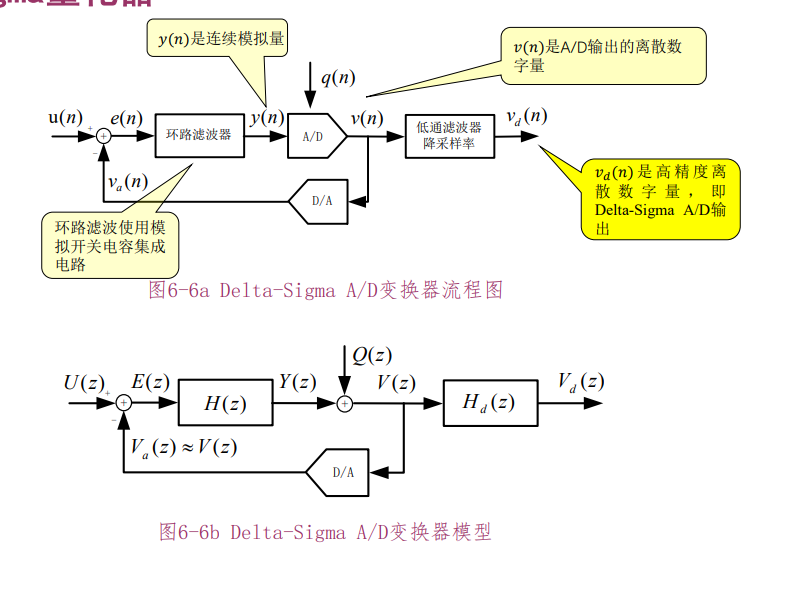
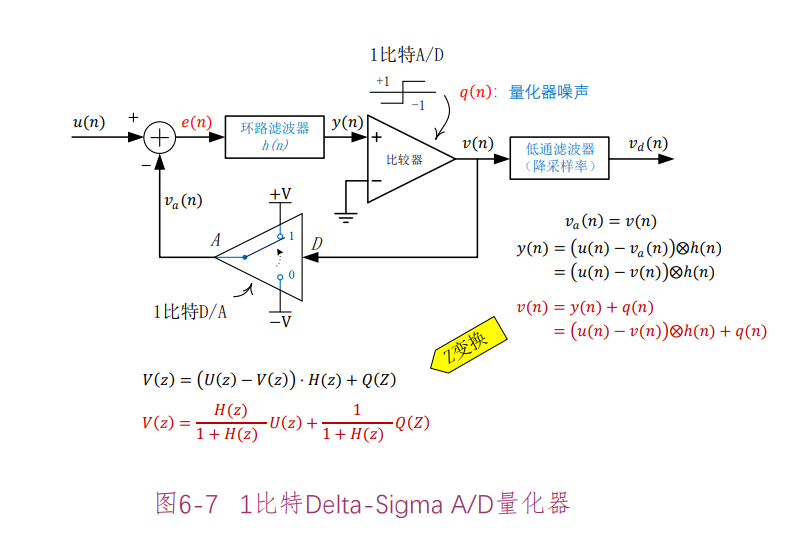
考虑 $D/A$ 变换器的增益为 1 的情况,此时 $V_a(z)\approx V(z)$ ,
$$ \begin{gathered} V(z)=[U(z)-V(z)]\cdot H(z)+Q(z) \\ [1+H(z)]\cdot V(z)=U(z)\cdot H(z)+Q(z) \\ V(z)=\frac{H(z)}{1+H(z)}U(z)\cdot+\frac{1}{1+H(z)}Q(z) \end{gathered} $$定义信号传输函数
$$ STF(z)=\frac{V(z)}{U(z)}\Bigg|_{Q(z)=0}=\frac{H(z)}{1+H(z)} $$定义超取样量化噪声传输函数
$$ NTF(z)=\frac{V(z)}{Q(z)}\Bigg|_{U(z)=0}=\frac{1}{1+H(z)} $$让 $H(z)$ 为低通,则 $STF(z)$ 是低通, $NTF(z)$ 是高通
$$ V(z)=STF(z)\cdot U(z)+NTF(z)\cdot Q(z) $$噪声整形(Noise-Shaping)技术: $NTF(z)$ 去掉了噪声能量的低频部分。接下来,只要经过低通滤波器 $H_d(z)$ ,就可以滤除高频部分的噪声能量,剩下的只有所需要的信号 $U(z)$ , $H_d(z)$ 的输出 $V_d(z)$ 的量化噪声可以小于直接用 A/D 量化器量化的噪声。
采用速度(超采样)换精度(高量化比特数),量化器的精度可以非常低,甚至可以用 1 bit 量化器。1 bit 量化器,就不存在 A/D 非线性问题。
超采样的好处:扩展了频带宽度,我们认为噪声的功率一定,当频带变宽,噪声功率谱的高度就降低了。
子带编码
含有多个频点信号分量的复合宽带信号
首先用一组滤波器将信号分解成若干子带信号
$$ \langle f_1(t),f_2(t)\rangle=\frac1{2\pi}\cdot\langle F_1(\omega),F_2(\omega)\rangle $$若 $\langle F_1(\omega),F_2(\omega)\rangle\approx0$ ,则采用子带滤波后,两个信号的相关性 $\langle f_1(t),f_2(t)\rangle$ 降低,对于这些不相关的子带信号独立编码可能提高编码效率。
比特数分配
$$ \sum_{k=1}^MR_k=R\\ \sigma_{r_k}^2=\varepsilon_{*k}^2\cdot2^{-2R_k}\cdot\sigma_{x_k}^2\\ \min_{R_k} \sigma_{r,SBC}^2=\sum_{k=1}^M\varepsilon_{*k}^2\cdot2^{-2R_k}\cdot\sigma_{xk}^2\\ $$解得
$$ R_{k,opt}=R/M+\frac12\log_2\frac{\sigma_{x_k}^2}{\left[\prod_{i=1}^M\sigma_{x_i}^2\right]^{1/M}}\\ \sigma_{r_k}^2=\varepsilon_{*k}^2\cdot2^{-2R/M}\cdot\left[\prod_{i=1}^M\sigma_{x_i}^2\right]^{1/M}\\ min\{\sigma_{r,SBC}^2\}=M\cdot\varepsilon_*^2\cdot2^{-\frac{2R}{M}}\cdot\left[\prod_{i=1}^M\sigma_{x_i}^2\right]^{\frac{1}{M}} $$每个子带的采样率变为总带宽的 1/M,总的信息比特速率为 $R \cdot f/M$ ,为了与 PCM 进行比较,假设 SBC 和 PCM 的编码速率相等:
$$ R_{PCM} \cdot f = R_{SBC} \cdot f / M\\ \Rarr R_{PCM} = R_{SBC}/M $$此时可推出 SBC 较于 PCM 的信噪比增益为
$$ max\{G_{SBC}\}=\frac{\sigma_{r,PCM}^{2}}{\sigma_{r,SBC}^{2}}=\frac{2^{-2R_{PCM}}\sigma_{x}^{2}}{M\cdot2^{-\frac{2R_{SBC}}{M}}\cdot[\prod_{k=1}^{M}\sigma_{xk}^{2}]^{\frac{1}{M}}}\\=\frac{2^{-\frac{2R_{SBC}}{M}}\sigma_{x}^{2}}{M\cdot2^{-\frac{2R_{SBC}}{M}}\cdot[\prod_{k=1}^{M}\sigma_{xk}^{2}]^{\frac{1}{M}}}=\frac{\sigma_{x}^{2}}{M\cdot[\prod_{k=1}^{M}\sigma_{xk}^{2}]^{\frac{1}{M}}}\\=\frac{\frac{1}{M}\sigma_{x}^{2}}{[\prod_{k=1}^{M}\sigma_{xk}^{2}]^{1/M}}=\frac{\frac{1}{M}\sum_{k=1}^{M}\sigma_{xk}^{2}}{[\prod_{k=1}^{M}\sigma_{xk}^{2}]^{1/M}} $$因此 SBC 的信噪比增益等于子带信号的算术平均和几何平均之比。
- 子带信号能量越大,则分配比特数越多;
- 最佳分配条件下,各个子带的量化噪声相同;
- 若各个子带能量相同,则子带编码的增益为1
多相正交滤波器组
用一组不同频率的余弦信号对低通滤波器进行调制,变成了带通滤波器组:
$$ H_i(z)=\sum_{n=-\infty}^{+\infty}h(n)\cdot cos\left(\pi(2i+1)\cdot\frac{n}{2M}\right)\cdot z^{-n}=\frac12F_i(z)+\frac12G_i(z) $$ $$ F_{i}\big(e^{j\omega}\big)=H(e^{j(\omega-\frac{\pi(2i+1)}{2M})}),\quad i=0,1,\cdots M-1\\G_{i}\big(e^{j\omega}\big)=H(e^{j(\omega+\frac{\pi(2i+1)}{2M})}),\quad i=0,1,\cdots M-1 $$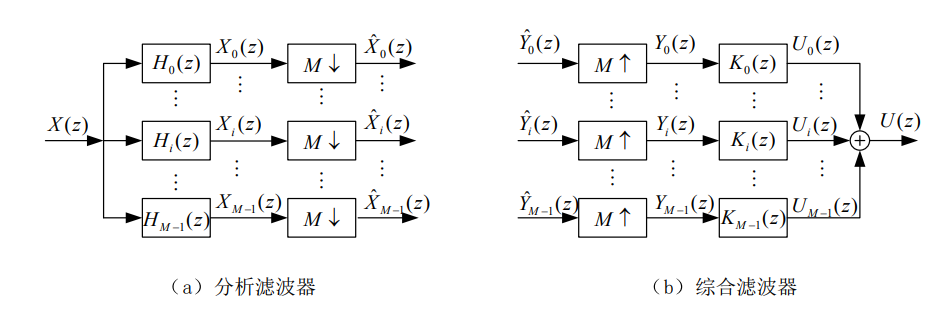
分析滤波器:子带滤波,降采样;
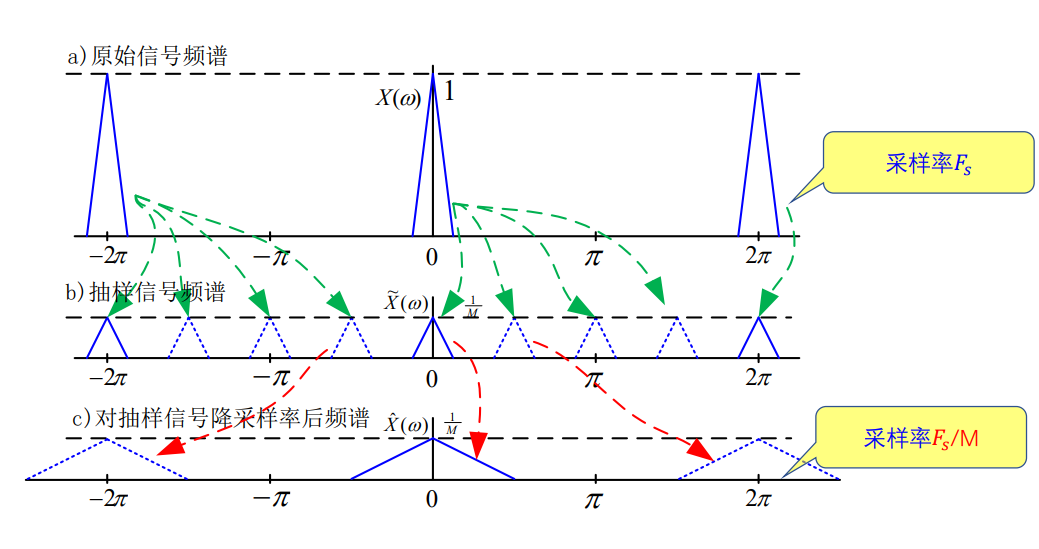
降采样率过程等价于:采样(b, 将非M倍数的采样点置为0) + 分频(c,抽取 M 倍数上的采样点形成新的信号)
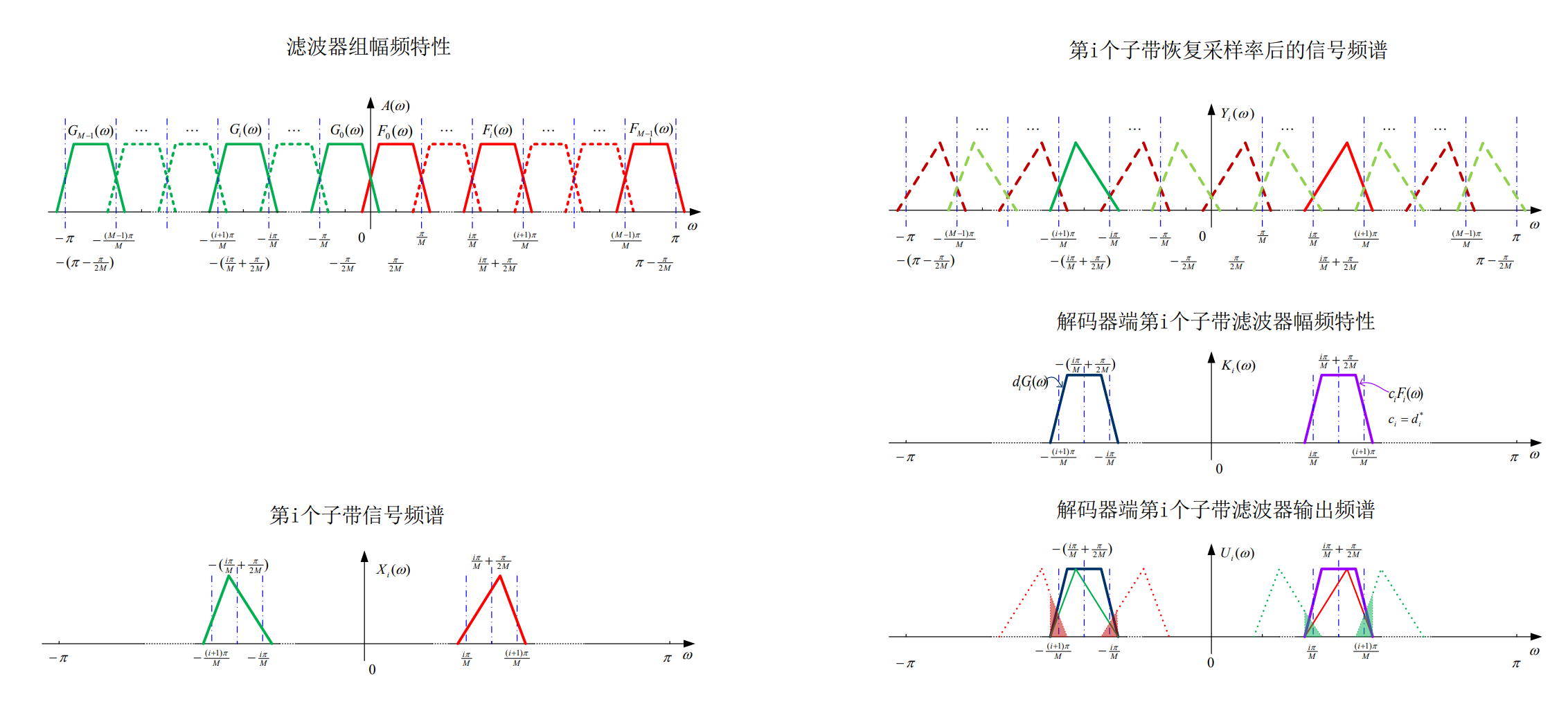
每个子带的输出会产生四种混叠干扰:
$$ \begin{aligned} U_i(e^{j\omega})& =K_i(e^{j\omega})\cdot Y_i(e^{j\omega}) \\ &\approx\frac1MK_i(e^{j\omega})\{a_iF_i(e^{j\omega})X(e^{j\omega})+b_iG_i(e^{j\omega})X(e^{j\omega})+ \\ &a_iF_i(e^{j(\omega+\frac{2\pi}M\cdot i)})X(e^{j(\omega+\frac{2\pi}M\cdot i)})+b_iG_i(e^{j(\omega-\frac{2\pi}M\cdot i)})X(e^{j(\omega-\frac{2\pi}M\cdot i)})+ \\ &a_iF_i(e^{j(\omega+\frac{2\pi}M\cdot(i+1))})X(e^{j(\omega+\frac{2\pi}M\cdot(i+1))})+b_iG_i(e^{j(\omega-\frac{2\pi}M\cdot(i+1))})X(e^{j(\omega-\frac{2\pi}M\cdot(i+1))})\} \\ &i=1\sim M-2 \end{aligned} $$为了解决升采样后的频谱混叠,在综合滤波器部分精确对消混叠信号:
$$ a_id_i=-a_{i-1}d_{i-1},\quad i>0 $$变换域编码
正交变换后编码:
$$ Y = AX $$正交变换满足能量守恒
$$ ||Y||^2 = ||X||^2 $$重建信号的误差等于变换域上量化器的误差
$$ E = Y - [Y]\\ ||X - [x]||^2 = ||E||^2 $$比特分配
假设 N 个输入样本组成一个矢量 X,变换域 Y 的每个分量用 $R_k$ 个比特量化
$$ R=\frac1N\sum_{k=0}^{N-1}R_k\\ \sigma_q^2=\sum_{k=0}^{N-1}\sigma_{q,k}^2=\varepsilon_*^2\cdot\sum_{k=0}^{N-1}2^{-2R_k}\sigma_k^2\\ \min \sigma_{q}^{2}=\frac{1}{N}\sum_{k=0}^{N-1}\sigma_{q,k}^{2} $$ $$ R_{k,opt}=R+\frac12\log_2\frac{\sigma_{x_k}^2}{\left[\prod_{i=1}^M\sigma_{x_i}^2\right]^{1/N}}\\ \sigma_{q}^2 = min\{\sigma_{q,k}^2\}=\varepsilon_*^2\cdot2^{-2R}\cdot\left[\prod_{i=1}^M\sigma_{x_i}^2\right]^{\frac{1}{N}} $$相比 PCM 的增益为
$$ \begin{gathered} G_{TC} =\frac{min\{\sigma_{r,PCM}^{2}\}}{min\{\sigma_{r,TC}^{2}\}}=\frac{\varepsilon_{*}\cdot2^{-2R}\cdot\sigma_{\chi}^{2}}{\varepsilon_{*}\cdot2^{-2R}\cdot\prod_{k=0}^{N-1}[\sigma_{k}^{2}]^{\frac{1}{N}}} \\ =\frac{\sigma_x^2}{\prod_{k=0}^{N-1}[\sigma_k^2]^{1/N}}=\frac{\frac1N\sum_{k=0}^{N-1}\sigma_k^2}{\prod_{k=0}^{N-1}[\sigma_k^2]^{1/N}} \end{gathered} $$最佳正交变换 - KL 变换
语音信号的参数编码
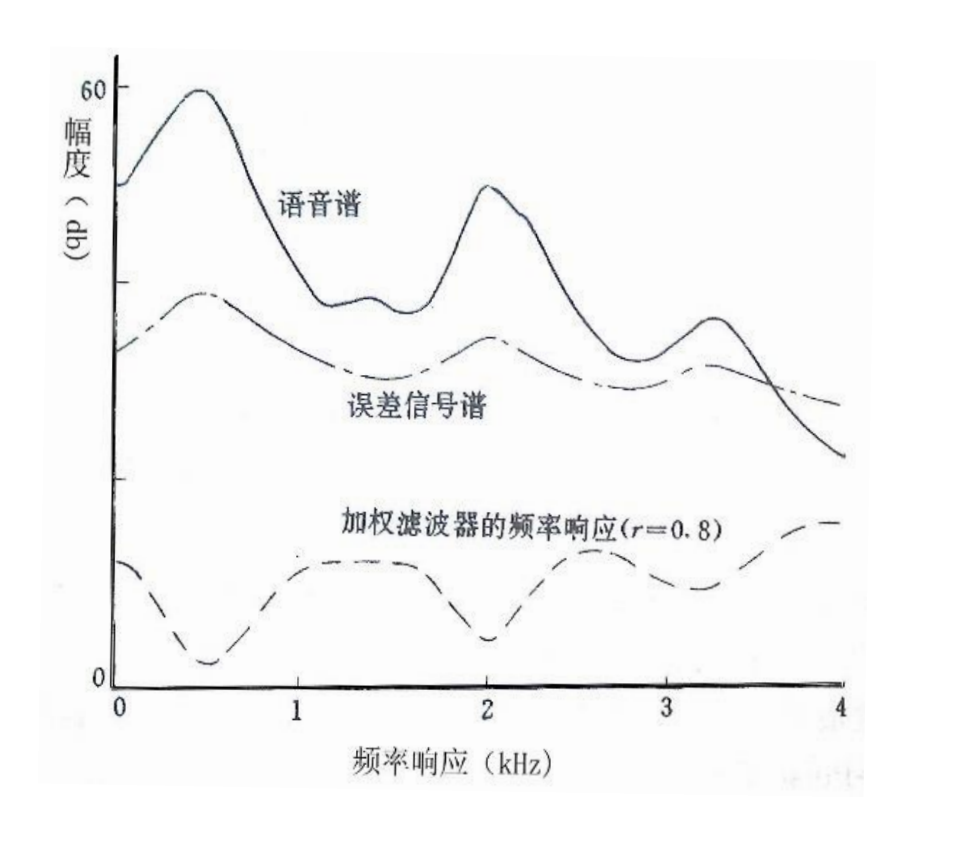
感觉加权滤波器
误差函数加权:
$$ J=\int_0^{f_s}\lvert s(f)-\hat{s}(f)\rvert^2\cdot\lvert w(f)\rvert^2df $$其中,加权滤波器满足
$$ \int_0^{f_S}|w(f)|df= Const. $$当误差函数最小的时候,应当保证
$$ |s(f)-\hat{s}(f)|^2\cdot|w(f)|=\frac{\gamma}{2}=\text{常数} $$可以选择如下的滤波器:
$$ w(z)=\frac{A(z)}{A\left(\frac{z}{\gamma}\right)}=\frac{1-\sum_{i=1}^P\alpha_iz^{-i}}{1-\sum_{i=1}^P\alpha_i\gamma^iz^{-i}},\quad0\leq\gamma\leq1 $$ $\gamma$ 为加权因子,在 0-1 之间。 $\gamma=0$ 时变成逆滤波器,其频谱包络的峰值点就是语音谱的谷值点。分析:语音信号是全极点模型产生的,即 $S(z) = GE(z)/A(z)$ ,与逆滤波器点频谱成反比。
多脉冲激励线性预测声码器
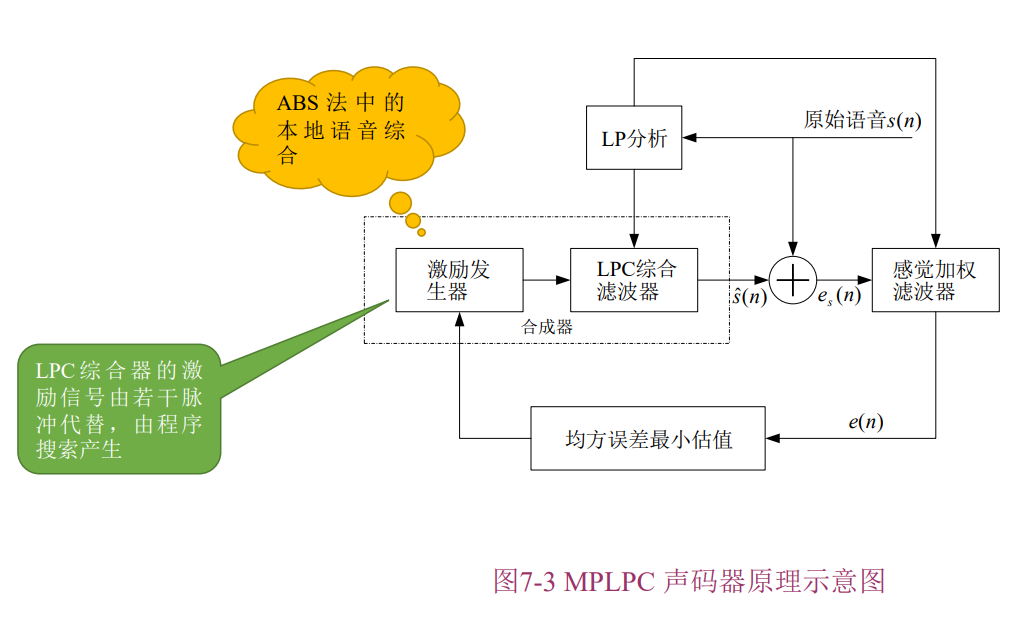
语音综合器的激励源有若干个不同位置和幅度的脉冲信号组成。
$$ \hat{s}(n)=\hat{s}_0(n)+\sum_{k=1}^Mg_kh(n-n_k) $$其中 $\hat s_0(n)$ 是 LPC 综合器的零输入响应。
$$ \begin{aligned}&e_{s}(n)=s(n)-\hat{s}(n)=s(n)-\hat{s}_{0}(n)-\sum_{k=1}^{M}g_{k}h(n-n_{k})\\&=\bar{e}(n)-\sum_{k=1}^Mg_kh(n-n_k)\end{aligned} $$用 $\bar{e}(n)=s(n)-\hat{s}_0(n)$ 表示输入语音减去零输入响应(受历史激励影响的部分)。
输入感觉加权滤波器,得到输出
$$ \begin{aligned}e(n)&=e_{s}(n)*w(n)=\left[\bar{e}(n)-\sum_{k=1}^{M}g_{k}h(n-n_{k})\right]*w(n)\\&=\bar{e}_{w}(n)-\sum_{k=1}^{M}g_{k}h_{w}(n-n_{k})\end{aligned} $$从而,得到感觉加权滤波器的误差函数
$$ E=\sum_{n=1}^Ne^2(n)=\sum_{n=1}^N\left[\bar{e}_w(n)-\sum_{k=1}^Mg_kh_w(n-n_k)\right]^2 $$选择合适的 $n_k$ , $g_k$ 使得上面的误差函数最小
$$ \frac{\partial E}{\partial n_j}=0,\quad j=1,\cdots M\\\frac{\partial E}{\partial g_j}=0,\quad j=1,\cdots M $$上面那个方程很复杂,会导出非线性的方程;
从下面的那个方程可以推出
$$ \sum_{k=1}^Mg_kR_{hh}(n_k,n_j)=R_{eh}(n_j),\quad j=1,\cdots M $$其中
$$ R_{eh}(n_j)=\sum_{n=1}^N\bar{e}_w(n)\cdot h_w(n-n_j)\\R_{hh}(n_k,n_j)=\sum_{n=1}^Nh_w(n-n_k)h_w(n-n_j) $$此时可改写最小均方误差
$$ E_{min}=\sum_{n=1}^N[\bar{e}_w(n)]^2-\sum_{k=1}^Mg_kR_{eh}(n_k) $$最优解的计算涉及到非线性方程的求解,不太现实。考虑采用次优搜索,一个一个求解。
当只有一个脉冲时
$$ g_1R_{hh}(n_1,n_1)=R_{eh}(n_1)\\ E_{min}=\sum_{n=1}^N[\bar{e}_w(n)]^2-g_1R_{eh}(n_1) $$消元得到
$$ E_{min}=\sum_{n=1}^N[\bar{e}_w(n)]^2-R_{eh}^2(n_1)/R_{hh}(n_1,n_1) $$接下来搜索 $n_1$ 使得上式最优化。解出 $n_1$ 后即可解出 $g_1$ 。
接下来一个个求解,每次都要把前面求解过的脉冲折算到零输入响应中,然后求解当前的结果:
语音信号修整与综合技术
短时谱分析
$$ \begin{gathered}w[n]=\begin{cases}\neq0&,&0\leq n<L\\0&,&\text{其它}\end{cases}\\X(p,k)=\sum_{n=-\infty}^{+\infty}x[n]w[p-n]e^{-j\frac{2\pi}{N}nk}\\x[n]w[p-n]=\left[\frac{1}{N}\sum_{i=0}^{N-1}X(p,k)e^{j\frac{2\pi}{N}nk}\right]\cdot R[p-n]\end{gathered} $$利用修正短时谱进行最小方差信号估计
首先计算短时谱
$$ X(p,\omega)=\sum_{m=-\infty}^{+\infty}x[m]w(p-m)e^{-j\omega m} $$对短时谱进行修正
$$ Y(p,\omega)=X(p,\omega)H(p,\omega) $$需要得到一个“有效”的短时谱,满足:
- 时域短时段有限长,非零段不超过窗函数 $w(p-n)$ 的范围
- 一致性约束,即不同的𝑝时刻 𝑌(𝑝,𝜔)所对应的时域短时段,若有部分重叠,那么在去除分析窗的加权影响后,在重叠的部分,它们应该是相等的。
实际上很难得到上述信号,可以通过最小方差准则逼近
$$ D[\hat{Y}(n,\omega),Y(n,\omega)]=\sum_{m=-\infty}^{+\infty}\frac{1}{2\pi}\int_{-\pi}^{\pi}\left|\hat{Y}(m,\omega)-Y(m,\omega)\right|^{2}d\omega $$其中
$$ \hat{Y}(p,\omega)=\sum_{m=-\infty}^{+\infty}\hat{y}[m]w(p-m)e^{-j\omega m} $$利用 Parseval 定理
$$ \begin{aligned}&D\big[\hat{Y}(n,\omega),Y(n,\omega)\big]=\sum_{m=-\infty}^{+\infty}\sum_{n=-\infty}^{+\infty}|\hat{y}_{m}(n)-y_{m}(n)|^{2}\\&=\sum_{m=-\infty}^{+\infty}\sum_{n=-\infty}^{+\infty}|\hat{y}(n)w(m-n)-y_{m}(n)|^{2}\end{aligned} $$变分法求得最小值
$$ \hat{y}[n]=\frac{\sum_{m=-\infty}^\infty w(m-n)y_m(n)}{\sum_{m=-\infty}^\infty w^2(m-n)} $$其中
$$ y_m(n)=\frac{1}{2\pi}\int_{-\pi}^\pi Y(m,\omega)e^{j\omega n}d\omega $$应用中,以周期 $T$ 分析
$$ \hat{y}[n]=\frac{\sum_{m=-\infty}^\infty w(mT-n)y_{mT}(n)}{\sum_{m=-\infty}^\infty w^2(mT-n)} $$如果 $w(n)$ 取三角窗的平方根
$$ w^2(n)=\begin{cases}1-\frac{|n-T|}{T}&,\quad0\leq n\leq2T\\\\0&,\quad\text{其它}\end{cases} $$若 n 此时为奇数, $T = (N-1)/2$ ,这时 $\sum_{m=-\infty}^{\infty}w^{2}(mT-n)=1$ ,可简化计算,如果频谱无修正,最优解为
$$ \hat{y}(n)=\frac{\sum_{m=-\infty}^\infty w(mT-n)[w(mT-n)x(n)]}{\sum_{m=-\infty}^\infty w^2(mT-n)}=\frac{x(n)\sum_{m=-\infty}^\infty w^2(mT-n)}{\sum_{m=-\infty}^\infty w^2(mT-n)}=x(n) $$若改变语音的速度, $p=k\cdot p^{\prime}$ ,满足 $|Y(p,\omega)|=|X(p^{\prime},\omega)|$ 。
$$ y_{p'}(n)=\frac{1}{2\pi}\int_{-\pi}^{\pi}Y(p',\omega)e^{j\omega n}d\omega=w(p'-n)x(n) $$让 $\tau_p=p-p^{\prime}=(1-1/k)\cdot p$ ,
$$ \begin{aligned}&y_p(n)=y_{p^{\prime}}(n-\tau_p)=w(p^{\prime}-n+\tau_p)x(n-\tau_p)\\&=w(p-n)x(n-\tau_p)\end{aligned} $$代入重建公式
$$ \hat{y}[n]=\frac{\sum_{m=-\infty}^\infty w^2(mT-n)x(n-\tau_{mT})}{\sum_{m=-\infty}^\infty w^2(mT-n)} $$让 $\sum_{m=-\infty}^{\infty}W(mT-n)= \sum_{m=-\infty}^{\infty}w^2(mT-n) =1$ ,
$$ \hat{y}[n]=\sum_{m=-\infty}^{\infty}W(mT-n)x(n-\tau_{mT}) $$